Ridge / Lasso regression

 

 

6.2 Shrinkage Methods

 

subset selection에서는 선형회귀를 적합하기 위해 Least Squares를 사용하였지만, 이제부터는 대안적인 방법으로 회귀계수 추정량에 제약(constraints)을 주거나 정규화(regularizes)시킬 것이다. 이는 회귀계수 추정량을 0으로 수축시키는 것과 동일한 의미를 가진다. 이러한 처리로 인해 추정량의 분산을 상당히 줄일 수 있다. 가장 널리 알려진 방법으로 Lasso와 Ridge가 있다. 

 

6.2.1 Ridge Regression

 

3장에서 다루었던 선형회귀에 대한 LS적합은 RSS를 최소로하는 추정량을 선택하는 방법이었다. Ridge 회귀는 RSS에서 추가된 항이 존재하며 이를 최소로하는 추정량을 사용한다. 

$\sum_{i=1}^n (y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij})^2 + \lambda \sum_{j=1}^p \beta_j^2$ = $RSS + \lambda \sum_{j=1}^p \beta_j^2$

 

minimize $ \left \{ \sum_{i=1}^n(y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij})^2 \right \}$

subject to $\sum_{j=1}^p \beta_j^2 \leq s$

 

$\lambda \geq 0$는 조절모수(tuning parameter)이다. 첫번째 항은 LS적합과 동일하게 작을수록 데이터에 잘 적합하는 의미를 가지며, 두번째 항은 shinkage penalty로 $\lambda = 0$이면, ridge 회귀계수는 OLS 추정량과 같아진다. $\lambda -> \infty$이면 penalty의 효과가 증가해 ridge 회귀계수 추정량은 0에 가까워진다. 

하나의 $\beta$ set만 가지지만, ridge는 $\lambda$ 마다 다른 set을 가지게 된다($\hat\beta_{\lambda}^R$  : $\lambda$에 의존). 따라서, 최적의 $\lambda$값을 찾는 것도 중요하며 이는 6.2.3에서 다룰 것이다. ridge는 $\beta_0$에 대해서는 적용되지 않는다. 즉, ridge는 y와 관련된 각 변수의 추정량을 수축시키는 것이 목적이다. $\beta_0$는 어디에서나  $x_{i1}=x_{i2}=\cdots=x_{ip}=0$일 때 y의 평균값을 가진다. 따라서, ridge를 수행하기 전 data matrix X를 중심화시킨다면(각 x들의 평균이 0이 됨.) , $\hat\beta_0 = \bar y = \sum_{i=1}^n\frac{y_i}{n}$이 될 것이다.

  

위의 그림은 Credit data에서 $\lambda$에 따른 ridge 회귀계수를 구한 것이다. 왼쪽그림에서 $\lambda$가 커질수록 회귀계수가 0으로 수축하는 것을 볼 수 있다. 오른쪽그림은 x축을 표준화 한 것으로 ridge회귀계수를 L2-norm($||\beta||_2=\sqrt(\sum_{j=1}^p \beta_j^2$)으로 나누어주면, $\lambda = 0$일 때는 (ridge 회귀계수 추정량이 OLS 추정량과 같아지므로) 1의 값을 가지고 $\lambda = \infty$일 때는 (ridge가 0이 되므로) 0의 값을 가진다.  

 

 OLS적합의 경우, X의 scale에 영향을 받지 않는다. (multiplying $X_j$ by a constant c simply leads to a scaling of the least squares coefficient estimates by a factor 1/c : X에 어떠한 상수 c를 곱하더라도 OLS 추정량은 1/c값으로 도출된다.) 즉, 예측변수들의 scale에 상관없이 $X_j\hat\beta_j$은 같을 것이다. 반면, ridge 추정량은 예측변수의 scale에 따라 크게 변할 수 있다. 따라서, 예측변수에 대해 표준화를 수행해준 후 ridge regression을 적용해야한다. 

 

$\tilde{x_{ij}} = \frac{x_{ij}}{\sqrt{\frac{1}{n} \sum_{i=1}^n(x_{ij}-\bar x_j)^2}}$

 

 

Ridge의 장점은 OLS와 비교했을 때, Bias-Variance trade-off로 설명할 수 있다. $\lambda$가 증가 했을 때, variance는 감소하고 bias는 증가하게 된다. 

 

보라색 선은 test MSE, 검정색 선은 Squared bias, 초록색 선은 Variance을 나타낸다. $\lambda$가 0일 때(OLS추정량), bias는 0이고 variance가 높다. $\lambda$가 증가할 때, Ridge 회귀계수의 수축(shrinkage)은 상당한 분산 감소를 가져온다(약간의 bias가 높아지면서). test MSE는 variance+bias를 나타낸 것이다. $\lambda$가 0-10일 때, 분산히 빠르게 감소하고 bias가 조금 높아졌다. 그 이후의 구간에서는 variance는 계속 감소하고 bias는 계속 증가하게 되는데 이런 경우 과소추정의 위험이 있다. 

 

 

일반적으로, 반응변수와 예측변수가 선형관계를 가지는 상황에서 OLS추정량은 낮은 bias와 높은 variance를 가질 것이다. 이는 training data의 작은 변화에도 추정량이 많이 바뀔 수 있음을 의미한다. 특히, 예측변수의 수(p)가 관측치 수(n)만큼 클때, OLS추정량은 극도로 변할 수 있다. (위의 6.5 그림이 p=45, n=50 인 경우임.) 

만약, p>n이라면 OLS 추정량은 유일한 해를 가지지 못하지만, ridge의 경우 잘 수행되며 ridge는 OLS 추정량이 높은 variance를 가지는 경우에 유용하게 사용된다. ridge는 또한 best subset selection보다 계산적으로 상당한 장점을 가진다. best subset selection은 적절한 p개를 찾기 위해 엄청난 계산량이 필요하게 된다. 하지만, ridge는 최적 $\lambda$를 찾으면 해당 $\lambda$에 대해 하나의 모형만 생성되며 절차도 비교적 빠르게 수행된다.

 

 

6.2.2 The Lasso

 

Ridge 회귀는 한가지 단점을 가지고 있다. 일부 변수를 선택하는 best subset, stepwise와는 달리, ridge는 모든 변수를 포함하고 있으며 shinkage penalty ($\lambda \sum \beta_j^2$)를 통해 모든 회귀계수를 0으로 수축시킬 것이다. ($\lambda ->\infty$가 아니라면 일부 변수를 정확히 0으로 수렴시킬수는 없을 것이다.) 

이는 예측정확도의 문제뿐만 아니라 해석을 할때에도 문제가 발생할 수 있다. 예를 들어, 데이터에 중요한 변수가 있다고 하자. 우리는 중요한 변수만 포함하는 모델을 만들어야 한다. 하지만, ridge는 중요한 변수를 포함한 모든 예측변수를 모형에 포함할 것이다. 즉, $\lambda$가 증가함에 따라 예측변수에 대한 회귀계수 추정량을 수축시킬뿐 완전히 배제시킬 수는 없다.(회귀계수가 완전히 0으로 수축하지않아 모든 변수가 살아있다는 것.)

 

Lasso는 ridge의 문제를 보안한 방법으로 다음의 목적함수를 최소로하는 추정량을 사용한다.

 

$\sum_{i=1}^n (y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij})^2 + \lambda\sum_{j=1}^p |\beta_j|$ = $RSS + \lambda \sum_{j=1}^p |\beta_j|$

 

위의 식은 다음과 같이도 나타낼 수 있다.

 

minimize $\left \{ \sum_{i=1}^n(y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij})^2 \right \}$

subject to $\sum_{j=1}^p|\beta_j| \leq s$

 

ridge의 shrinkage penalty에서 L2-norm을 L1-norm($\sum |\beta_j|$)으로 변경해준 형태이다. lasso 회귀도 ridge와 마찬가지로 회귀계수를 0으로 수축하려는 성질을 가진다. 그러나, lasso의 경우에 L1-norm는 $\lambda$가 무한대가 아닌 충분히 큰 값을 가질때도 추정량을 완전히 0으로 수축시킬 수 있다. 그 결과, lasso 회귀로부터 생성된 모형은 ridge 보다 해석하기 더 쉬워지게 된다. 회귀계수 추정량을 완전히 0으로 수축시키는 lasso의 성질로 sparse model이라고도 불린다. 이는 일부 변수를 선택한 효과를 가지기 때문에 듬성듬성한 모형이라는 의미를 가진다. 최적의 $\lambda$를 찾는 문제는 6.2.3에서 다룰 것이다. 

 

$\lambda$에 따라 lasso의 standardized coefficients를 나타낸 것으로 $\lambda = 0$일 때 OLS추정량와 같은 결과를 가진다. $\lambda$가 충분히 커지면, 모든 회귀계수 추정량이 0으로 수축하므로 null 모형이 된다. 

 

정리하면, ridge와 lasso 모두 회귀계수 추정량을 0으로 수축시키지만 ridge의 경우 $\lambda$가 무한대를 가지지 않는 이상 모든 변수들이 0으로 완전히 수렴하지 못해 결국 모든 변수를 포함하는 모형을 가지게 된다. 반면, lasso는 적절히 $\lambda$가 큰값을 가지기만 하면 일부 추정량을 0으로 완전히 수축시키므로 변수선택효과를 가지게 된다. 

 

 

ridge와 lasso의 목적함수에서 두번째 식을 보면 L1-norm 또는 L2-norm이 특정값 s보다 작다는 조건하에 RSS를 가장 최소로 하는 회귀계수 추정량을 찾는다. 이를 밑의 그림으로 표현할 수 있다. (구현, 이해를 위해 p=2일 때를 고려.) 

lasso의 경우 $|\beta_1| + |\beta_2| \geq s$의 제약조건에 의해 다이아몬드 구간에 놓여져 있는 점들 중 가장 작은 RSS값을 가지는 회귀계수를 찾는것이고, ridge는 $\beta_1^2 + \beta_2^2 \geq s$의 제약조건에 의해 원 구간에 놓여져 있는 점들 중 가장 작은 RSS값을 가지는 회귀계수를 찾는 것이다. 

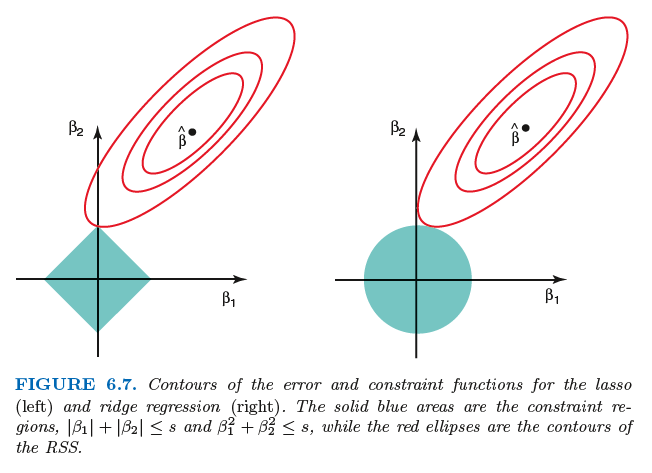
s가 극도로 큰 값을 가지면 제약조건의 의미를 잃게된다. 이는 위의 하늘색 영역이 커지게 되면 RSS를 작게해주는 추정량도 따라 커지게 되기때문이다. 예를 들어, 영역이 OLS추정량이 있는 곳을 포함하게 된다면, ridge와 lasso의 회귀계수는 OLS 추정량과 같아질 것이다.

 

위의 그림을 통해 왜 Lasso는 회귀계수를 완전히 0으로 수축시킬 수 있는지 설명할 것이다. 먼저 $\hat\beta$ 주변의 빨간선 타원은 RSS를 의미하며, 같은 선에 존재하는 $\beta$의 조합은 모두 같은 RSS를 가진다. 오른쪽 그림을 먼저 보면, ridge에 대한 그림으로 제약조건식이 제곱식의 형태이기 때문에 RSS와 맞닿는 점(point)이 $\beta_2$축 상에 존재하지 않게 된다. 반면, lasso의 제약조건식은 절댓값의 형태이므로 RSS와 맞닿는 점(point)가 $\beta_2$축 상에 존재하기 때문에 $\beta_1= 0$의 값을 가지게 된다. 이를 고차원으로 확장하면 동시에 많은 회귀계수 추정량들이 0으로 수축시킬 것이다. 

 

- Comparing the Lasso and Ridge Regression

 

ridge와 비교했을 때 lasso는 변수선택 효과를 가지므로 모델 해석력이 더 좋을 수 있다. 하지만, 정확도까지 좋다고 할 수 있을까 ? 왼쪽그림은 앞의 ridge에서 다루었던 데이터를 이용하여 lasso의 bias, variance, test MSE를 나타낸 것이며, 오른쪽 그림은 ridge와 lasso 적합에 대해 정확도에 따른 test MSE를 나타낸 것이다. (여기서, lasso 회귀적합 결과는 45개의 예측변수를 모두 0으로 수축시킨 모형이다, 영모형)  실선이 lasso, 점선이 ridge를 나타냄. bias 측면에서는 두 모형이 거의 동일해보이지만, variance 측면에서는 ridge가 더 작은 값을 가지게 된다. 따라서, test MSE는 ridge가 더 작으므로 해당 데이터에 대해서는 ridge 회귀를 적합하는 것이 적절해 보인다. 이는 일반화된 결과가 아닌 데이터에 따라 적절한 모형이 다를 수 있음을 인지하자. 

 

다음은 lasso 회귀 적합모형이 영모형(Null model)이 아닌 2개만 살아있는 모형인 경우이다. 

오른쪽 그림을 보면, lasso회귀를 적합한 모형이 전체적으로 ridge보다 뛰어난 것을 볼 수 있다. 두 개의 결과를 보면, 어떠한 적합모형이 더 뛰어나다고 할 수 없음을 알 수 있다. 일반적으로 lasso는 상대적으로 예측변수들 중 작은 일부분의 예측변수가 큰 회귀계수를 가지고 나머지 예측변수가 작은 회귀계수를 가지거나 거의 0과 동일한 상황에서 우수한 성능을 가질 수 있다. ridge는 예측변수들의 회귀계수가 대략 동일한 크기를 가지는 상황에서 우수한 성능을 가진다. 

 

ridge와 마찬가지로 lasso도 OLS 추정량이 높은 variance를 가질 때, 약간의 bias는 감안하면서 variance를 대폭줄 일 수 있다. 결론적으로 OLS보다는 더 우수한 정확도를 가지게 될것이다. 

 

 

- A Simple Special Case for Ridge Regression and the Lasso

 

ridge와 lasso의 효과에 대해 더 나은 결과를 얻기 위해, 간단하게 특별한 경우를 생각해보자. (n=p 이며, 대각성분이 1인 대각행렬 X 가 존재.) 또한 문제를 간단하게 하기 위해 절편은 고려하지 않는다고 가정할 것이다. 이러한 가정을 가지고 OLS 적합의 목적함수는 다음과 같이 나타낼 수 있다. 

$\sum_{j=1}^p (y_j - \beta_j )^2$

 

이러한 경우 OLS, Ridge, Lasso 추정량은 다음과 같다. 

$\hat\beta_j =y_j$

$\hat\beta_j^R =\frac{y_j}{(1+\lambda)}$

$\hat\beta_j^L = \left\{\begin{matrix}
 y_j-\lambda/2   & if \ y_j > \lambda/2 \\ 
 y_j-\lambda/2 & if \ y_j > \lambda/2 \\ 
 0 & if \ |y_j| \leq \lambda/2
\end{matrix}\right.$

ridge는 같은 비율로 OLS추정량을 수축시키고 있으며, lasso는 $y_i$가 $\lambda/2$보다 작을 경우에만 0으로 완전히 수렴시킨다. lasso에 의해 수축된 타입을 soft-thresholding 이라고 부른다(그냥 명명한듯). 이러한 특별한 경우를 봤을 때도 lasso만 일부 변수를 0으로 완전히 수렴시킨다는 것을 다시 한번 확인할 수 있다. 

일반적인 행렬 X에 대해서는 다소 복잡할 수 있지만 아이디어는 여전히 동일하다. 

 

"ridge 회귀는 모든 차원에 대해서 같은 비율로 회귀계수를 수축시키지만, lasso 회귀는 비슷한 정도로 모든 회귀계수를 수축시키면서 충분히 작은 회귀계수에 대해서는 0으로 수축시켜버린다."

 

 

6.2.3 Selecting the Tuning Parameter

 

Subset Selection에서 어떤 예측변수 조합들 중 최적모형을 찾는 것 처럼, Ridge와 Lasso는 $\lambda$를 조정하여 최적모형을 찾는다. 과정에서 Cross-Validation을 사용한다. 

[1] 고려할 $\lambda$의 범위(grid)를 선택한다.

[2] 각 $\lambda$값에 대해 cross-validation error를 구한다.

[3] error를 가장 작게 해주는 $\lambda$값을 선택한다. 

[4] 마지막으로, 선택된 $\lambda$값을 이용해 모형을 재적합시킨다. 

 

 

6.3 Dimension Reduction Methods

 

지금까지 얘기했던 변수선택법과 원 예측변수(original predictors)를 이용하여 정의되었다. 다른 접근법으로 차원 감소법이 존재하는데 이는 p+1개의 회귀계수를 추정하는 문제를 m+1개를 추정하는 문제로 감소화시키는 것이 아이디어이다.

원 예측변수를 변형시킨 상태에서 OLS를 적합해보자. $Z_1, Z_2, \cdots, Z_m (M<p)$ 은 원 예측변수 p개의 선형결합을 나타내며 다음과 같다.

$Z_m = \sum_{j=1}^p \phi_{jm}X_j$

여기서, $\phi_{1m}, \phi_{2m}, \cdots, \phi_{pm}, m=1,\cdots, M$ 은 미지의 상수이며, 이를 통한 선형회귀모형은 다음과 같다. 

$y_i = \theta_0 +\sum_{m=1}^M \theta_m z_{im} +\epsilon_i , i=1,\cdots, n$

 

$\theta_0, \cdots, \theta_M$은 회귀계수를 의미하며, 각 $\phi$값들이 넓은 범위에서 선택된다면, 차원 감소를 통한 선형회귀는 원 변수에 대한 OLS보다 좋은 성능을 가질 수 있다. 

 

변형된 예측변수를 이용한 선형회귀식에서 두번째 항을 전개하면 다음과 같다. 

$\sum_{m=1}^M \theta_m z_{im} = \sum_{m=1}^M \theta_m \sum_{j=1}^p \phi_{jm}x_{ij} = \sum_{j=1}^p\sum_{m=1}^M\theta_m \phi_{jm}x_{ij} = \sum_{j=1}^p \beta_j x_{ij}$

 

여기서, $\beta_j = \sum_{m=1}^M\theta_m\phi_{jm}$ 이다. 즉, 이는 원 변수를 이용한 선형회귀의 특별한 경우라고 생각할 수 있다. 차원축소법은 회귀계수를 위와 같은 형태로 제한하는 역할을 한다. 

변형된 예측변수를 만들기 위한 $\phi_{jm}$의 선택은 각 축소법에서 다르게 수행되며, 지금부터 2개의 축소법인 principal components analysis (PCA) 와 partial least squares 에 대해 알아보자.

 

 

6.3.1 Principal Components Regression

 

PCA는 고차원의 데이터 셋에서 저차원의 셋으로 축소시키는 유명한 접근법이다. PCA는 10장의 비지도 학습에서 자세히 다뤄질 것이며, 여기서는 회귀에서 어떤 방식으로 사용되는지 정도만 집고 넘어가고자 한다. 

first principal component direction은 데이터가 가장 많이 변화하는 방향이다. 위의 그림에서 초록색 선을 의미하며, 눈으로 봐도 높은 분산을 가지는 것을 알 수 있다. 만약, 해당 선으로 관측값들이 사영(projected)한다면, 사영된 관측값도 높은 분산을 가지게 될 것이다. 

파란 점선은 second principal component를 의미하며 관측값을 해당 주성분에 사영시키면 작은 분산을 가지게 될 것이다. 

 

첫번째 주성분을 수학적으로 나타내면 다음과 같다. 

 

$Z_{ㅑ1} = 0.839 \times (pop_i00-\bar{pop}) + 0.544 \times (ad_i-\bar{ad})$

 

$\phi_{11} = 0.839, \phi_{21} = 0.544$는 주성분계수이며, 방향(direction)을 의미한다. $\bar{pop}, \bar{ad}$는 각 변수의 평균을 나타내며, 주성분의 아이디어는 $\phi_{11}+\phi_{21}=1$을 만족하는 pop과 ad변수 간의 모든 가능한 조합 중에서 $Var(Z_1)$을 최대로 하는 계수를 찾는 것이다.

$z_{11}, z_{21}, \cdots, z_{n1}$ 은 주성분의 값(principal component scores)으로 정의된다. PCA vector의 또 다른 해석으로는 데이터와 가장 가까운 선으로 정의할 수 있으며, 사영된 관측값이 원자료 관측값과 가능한 가까워지는 방향으로 첫번째 주성분이 만들어진다. 

 

The Principal Components Regression Approach

 

주성분 회귀의 접근은 M개의 주성분을 이용하여 OLS를 적합하는 것이다. 즉, 원 예측변수를 축소시킨 형태인 주성분 M개만으로도 데이터의 변동을 대부분 설명할 수 있다는 것이 주성분 회귀의 아이디어이다.

주성분 회귀는 예측변수가 대부분의 변동을 가지는 방향 즉, 주성분이 Y와 관련된 방향이라고 가정한다. 이 가정을 만족한다면, 주성분 회귀가 더 나은 결과를 가져올 수 있다. 이는 p개의 예측변수에 대한 대부분의 정보는 M개의 주성분에 포함되어 있으며 m개의 회귀계수를 추정함으로써 과적합을 방지할 수 있기 때문이다. .

위의 그림은 ridge, lasso를 적합한 결과인 Figure 6.8 / Figure 6.9 와 같은 데이터(n=50, p=45)에 대해 주성분 회귀를 적합한 결과이다. 왼쪽 그림은 p개의 예측변수를 이용하였으며, 오른쪽 그림은 2개의 예측변수만을 사용하여 주성분회귀를 수행하였다. 상대적으로 왼쪽 그림의 PCR의 성능이 나쁜 것은 Y를 모델링하기 위해 많은 주성분이 생성되었기 때문이다. 해당 데이터에 대해서는 PCR이 ridge와 lasso 만큼 좋은 성능을 가지지는 못한다. 다음 그림을 보자.

 

위 그림은 PCR에 더 유리하도록 설계된 다른 시뮬레이션 데이터로부터의 결과이다. 주성분을 많이 사용할수록 bias는 감소하지만 variance는 증가하며, 이는 위의 왼쪽 그림과 같이 전형적인 U자 모형의 MSE를 가지게 된다. 따라서, 적절한 주성분의 갯수를 찾는 것이 중요하다. 

위의 예제에서 최적의 주성분의 수는 5개인 것으로 보여진다. 3개의 방법들 모두 고전적인 선형회귀에 비해서 상당한 성능 향상을 보여주지만, 그 중 PCR과 ridge의 성능이 두드러지게 나타난다. 

( + PCR은 lasso보다는 ridge와 밀접한 관련이 있는데 이는 ridge가 모든 변수를 사용하여 적합하기 때문이며, ridge는 PCR의 연속형 버전이라고 할 수 있다. - 자세한 설명은 Elements of Statistical Learning 을 참고! ) 

 

PCR은 소수의 주성분이 Y와의 관계뿐만 아니라 예측변수들의 대부분의 변동을 충분히 표현할 수 있는 경우에 좋은 성능을 보여준다. 여기서 주의할 점은 p개의 예측변수 대신 M개의 주성분을 사용했다고 해서 변수선택법이라고 생각해서는 안된다. 이는 PCR에서 사용된 M개의 주성분은 원래의 예측변수의 선형조합으로 이루어졌기 때문이다. 

 

 

위에서 적절한 M개의 주성분을 찾는 것이 중요하다고 언급하였다. 일반적으로 교차타당법을 이용하여 M을 선택하게 된다. 오른쪽 그림이 Credit 데이터(p=11)에 대해 교차타당법을 사용하여 얻어진 결과로 가장 작은 MSE를 가지는 주성분의 수는 10개인 것으로 보인다. 즉, 차원 축소가 거의 수행되지 않았다.

PCR을 수행할 때, 주성분 생성 이전에 각 예측변수들을 표준화를 수행해야한다(scale을 맞추기 위함). 표준화를 수행하지 않으면 높은 분산을 가지는 변수가 주성분에 큰 영향을 미치기 때문에 결과적으로 최종 PCR 모델에 영향을 미치게 된다. 

 

 

6.3.2 Partial Least Squares

 

PCR은 차원을 축소하는 방법(PCA)를 이용해 회귀를 적합한다. 주성분은 $X_1, X_2, \cdot, X_3$ 을 가장 잘 표현해주는 방향(즉, 주성분)으로 생성된다. 주성분은 Y와는 상관없이 만들어지기 때문에, PCR은 비지도 학습 접근에 해당한다. 이는 PCR의 단점으로도 이어질 수 있는데, "예측변수를 가장 잘 설명하는 방향(또는 주성분)을 형성한다고 해서 그 주성분이 반응변수를 가장 잘 예측할 것이라는 보장이 없다" 라는 것이다. 따라서, PCR의 대안으로 지도 학습 접근법인 PLS이 제안되었다. PLS는 PCR과 마찬가지로 차원을 축소하는 방법이지만, 반응변수와의 관계를 이용하여 주성분을 생성하며 이러한 점에서 지도 학습 접근이라고 생각할 수 있다. 간단히 말하자면, PLS 는 반응변수와 예측변수를 둘 다 설명해줄 수 있는 주성분을 생성하는 것이 목적이다.

 

주성분을 계산하는 방법은 PCR에서 제시했던 식과 동일하다. 즉, $Z_m = \sum_{j=1}^p \phi_{jm}X_j$. 다만, $\phi_{jm}$의 크기는 Y와 $X_j$의 상관 관계에 비례하게 된다. 따라서, Y와 가장 큰 상관을 가진 변수에 대해서는 높은 가중치를 부여해 준다. PLS의 주성분은 PCA만큼 예측변수의 정보를 가지고 있지는 않지만, 반응변수를 설명하는 데에 더 효과적이다. PLS의 두번째 주성분을 생성하기 위해서는 먼저 $Z_1$에서 각 변수를 회귀시키고 잔차를 취하여 $Z_1$에 대한 각 변수를 조정한다. 이러한 잔차는 첫번째 PLS 주성분으로 설명되지 않은 나머지 정보로 해석할 수 있다. 

두번째 주성분은 첫번째 주성분과 직교하도록 구해진다( 즉, 주성분간 상관 = 0 ).  이러한 방식으로 M번 반복하여 총 M개의 PLS 주성분을 만들며, OLS 적합을 통해 PLS 모형을 구축할 수 있다. 

PCR과 마찬가지로 PLS 주성분의 계수는 일반적으로 교차타당법에 의해 결정되며, PLS를 수행하기 전 예측변수와 반응변수를 모두 표준화하는 것을 잊지말자.

 

실제로, PLS는 ridge나 PCR보다 우수한 성능을 가지지 못하는 경우가 많다.

 

 

 

 

 

 

 

( 출처 )

An Introduction to Statistical Learning with Applications in R (Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani)