다중검정(multiple testing)의 문제
Note) 다중 비교(Multiple comparison), 다중 검정(Multiple testing), 사후 분석(Post-Hoc)이 같은 의미로 통용되고 있지만, 사실 이는 같은 것이 아니다 !
1. 다중 검정
다중 검정은 여러 개의 가설검정을 동시에 수행하는 것이다. 예를 들어, 증상이 다른 두 환자 집단 간에 유의한 변수들(ex. 유전자 변수들)을 식별하기 위해 유전자의 갯수만큼의 가설을 검정하는 것이다. 고전적인 가설 검정 방법은 단일 가설을 검정하는 것에 관심이 있었지만, 방대한 데이터가 많이 생성됨에 따라 다중 검정도 주목을 받고 있다.
그 안에 흔히 분산분석(ANOVA) 후 그 결과가 유의한 경우에 한해 어떤 처리간 평균이 다른지 밝히기 위해 동시에 수행되는 다중 비교가 그 안에 속한다.
2. 다중 검정의 문제
동시에 m개의 가설검정을 수행한다는 사실을 고려하지 않고 진행하면, 많은 Type I error가 발생하게 된다. 자세히 설명하면, 단일 검정에서 p-value가 0.01 보다 작을 때 귀무가설을 기각한다고 하면 기각된 가설이 false positive일 가능성이 1% 임을 의미한다. 이제 m개의 가설을 다중 검정할 때, m개의 가설에 대해서는 false positive일 가능성이 0.01 $\times$ m 될 것이다. 즉, 가설의 수가 m = 10000 이라면, 100개의 가설에 대해 잘못된 기각을 내릴수도 있는 것이다. 즉, 많은 Type I error를 발생시킨다.
과정) 단일 검정을 수행할 경우, 귀무가설이 참일 때 유의수준 5% 하에서 올바르게 판단할 확률은 $(1-0.05)=95%$ 이므로 3개의 가설을 모두 동시에 올바르게 판단할 확률은 $(1-0.05)^3 \approx 0.857$ 이다(곱의 법칙 : 두 사건이 동시에 발생할 경우의 수는 곱으로 나타낸다). 반대로 생각해보면, 어떠한 가설 하나라도 잘못된 판단(귀무가설을 기각하는 판단)을 내릴 확률이 $1-(1-0.05)^3 \approx 0.143$ 라는 의미이고, 총 15%의 유의수준을 적용한 것과 같게 된다.
즉, 각각의 가설에 대해 유의수준 $\alpha$(1종오류)인 검정을 동시에 수행할 경우 전체오류율(1종오류)이 매우 커지게 된다. 이를 다중 검정의 문제라고 하며, 전체오류율을 유지하는 방법이 필요하다. 대표적으로 FWER을 통제하는 방법, FDR을 조절하는 방법이 있다.
위에서 두 가지의 1종 오류가 등장했는데 용어정리를 먼저 해보도록 한다. 다수의 검정을 동시에 수행할 경우 발생하는 1종오류는 "실험별 오류율(experiment-wise error rate or family-wise error rate)" 라고 하며, 그 안에 개별 검정에 대한 1종 오류는 "비교별 오류율(comparison wise error rate or testwise error rate)" 이다. 이들의 관계는 다음과 같다.
$\alpha_f = 1-(1-\alpha_c)^m$
가설의 개수(m)가 크면 근사적으로 $\alpha \approx m \times \alpha_0 $ 이 된다.
$\alpha_f$ : family-wise error rate
$\alpha_c$ : comparison wise error rate$
$m$ : 가설 수
(1) FWER(Family-wise type 1 error rate)
Type I error rate는 귀무가설이 참인 상황에서 귀무가설을 기각할 확률을 의미하며, FWER은 m개의 가설검정을 수행할 때 적어도 한 개의 Type I error를 발생시킬 확률을 의미한다. 이를 더욱 형식적으로 표현하기 위해, m개의 가설검정을 수행한 결과를 제시한다.
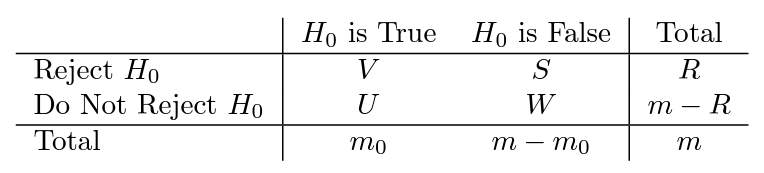
- V : Type I error(=false positive)의 수
- S : true positive의 수
- U : true negative의 수
- W : Type II error(=false negative)의 수
위 정의를 이용하여 FWER을 표현하면 다음과 같다.
$FWER = Pr(V \leq 1)$
= $1- Pr(V = 0)$
= 1 - 어떠한 가설도 잘못 기각하지 않을 확률
= 1- 모두 다 잘 기각시킬 확률
만약, m=1이라면 $FWER(\alpha) = 1-(1-\alpha)^1 = \alpha$이고 Type I error rate와 같게 된다. 그러나, 가설의 수가 m=100인 독립적인 검정을 수행하면, $FWER(\alpha) = 1-(1-\alpha)^{100}$ 이다. 예를 들어, $\alpha$ = 0.05면 $FWER = 1-(1-0.05)^{100} = 0.994$이다. 즉, 무조건 적어도 1개의 Type I error가 발생함을 의미한다.
우리는 이러한 FWER을 전체오류율로 보고 통제를 해야한다. FWER을 통제하는 방법으로 Bonfferoni, Holm, Westfall-young 검정이 존재한다. 또한, 특정 상황에서 FWER을 통제하는 방법으로 선호되는 Tukey's 방법과 Scheffe's 방법을 간단히 소개할 것이다.
- Bonferroni 검정
Bonferroni 검정은 개별 유의수준을 $\alpha/m$로 조정하여 개별 검정을 수행함으로서 전체오류율 FWER이 $\alpha$ 이하가 되도록 통제하는 방법이다. 하지만, Bonfferoni 검정은 가설의 수가 많아지면 개별검정의 유의수준이 작아지기 때문에 귀무가설을 잘 기각시키 않아 매우 보수적이다(= True positive를 잡지않아 False negative를 발생시킴, Type II error가 증가함). 실제 분석에서 개별 검정의 결과로 주어지는 p-값들은 이들 검정 방법들에 의해 수정된 값(adjusted p-value)으로 제공되며, 이는 FWER과 비교하여 검정을 수행하면 된다.
- Holm's Step-Down 검정
Bonferroni 검정의 단점을 보안한 방법으로 FWER을 통제하면서 본페로니 검정보다 덜 보수적인 방법이다. 귀무가설을 더 기각시키면서 Type II error를 줄인다. 따라서 검정력이 증가한다. 홈 검정의 과정을 다음과 같다.

Holm 검정은 개별 검정의 p-값을 순차적으로 나열한 뒤( i=1, ..., m , m=가설의 수) 유의수준 $\alpha/(m+1-i)$을 각각 다른 p-value cutoff 으로 부여하는 방법이다. 따라서 Bonfferoni보다 기각역이 크기 때문에 덜 보수적이다. 통계량 T이 큰 검정부터 (=p-값이 작은 검정) 귀무가설 기각 여부를 판단하기 때문에 Step-down방법이라고 한다.
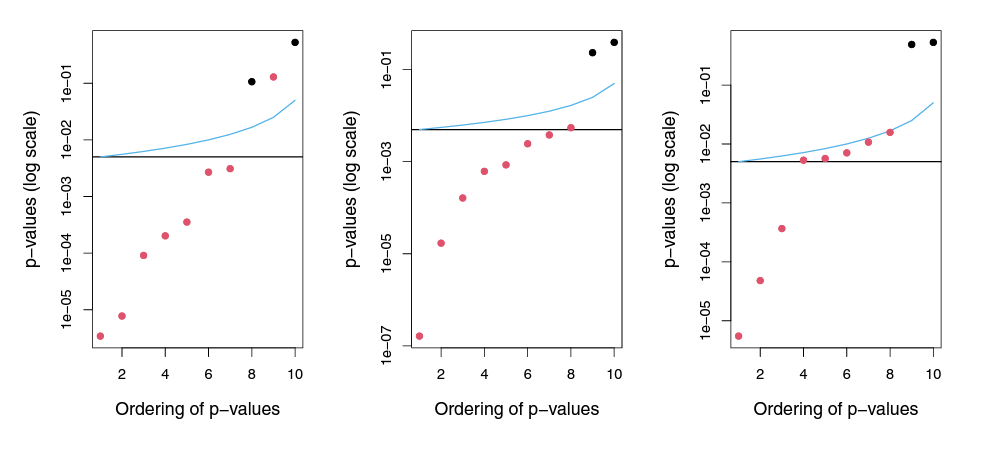
holm검정에 의한 FWER은 항상 본페로니 검정의 FWER보다 높게 위치한다. 따라서, 본페로니보다 항상 더 많은 귀무가설을 기각하며, 두 FWER 사이에 있는 p-value는 holm검정에 의해서만 기각된다. 왼쪽 그림에서, 본페로니와 holm검정은 false인 귀무가설 8개 중 7개를 잘 기각시켰다(= true positive). 중간 그림에서 holm검정은 false인 귀무가설 8개를 모두 잘 기각시켰으나 본페로니 검정은 7개를 기각시켰다. 오른쪽 그림에서는 holm검정은 false인 귀무가설 8개를 모두 잘 기각시켰으나 본페로니 검정은 3개만 기각시켰다. 하지만, 모든 예시에서 Type II error는 발생하지 않았다.
- Tukey's 검정과 Scheffe's 검정
정리하면, 본페로니 검정과 holm 검정은 m개의 다중검정을 수행할 때 FWER을 통제하길 원하는 상황에서 주로 사용된다. 위 방법들은 귀무가설, 검정통계량의 종류, p-value간의 독립에 대해 어떠한 가정도 할 필요가 없다. 하지만, 특정 상황에서는 Tukey 검정과 Scheffe 검정을 이용하여 FWER을 통제함으로써 더 높은 검정력을 가질 수 있다.
이는 우리가 흔히 알고 있는 다중비교의 상황을 생각하면 쉽다. m개의 가설이 독립적이지 않고 서로 연관되어 있는 경우 (즉, 1집단의 평균과 2집단의 평균이 비슷하고 1집단의 평균과 3집단의 평균이 비슷하다고 해보자. 그럼 2집단과 3집단의 평균도 비슷하다는 결론이 도출되는 경우)에 Tukey 검정과 Scheffe 검증을 이용하면 덜 보수적으로 수행할 수 있다.
예를 들어, G=6개의 평균을 비교하는 검정($H_0 : \mu_1 = \mu_2 = \mu_3 = \mu_4 = \mu_5 != \mu_6$)를 생각해보자. 쌍별 비교를 위해 총 m=G(G-1)/2 = 15개의 가설검정을 수행해야하며, 10개는 참인 귀무가설이고 5개는 거짓인 귀무가설을 의미한다.

각 그림에서 Tukey 검정은 항상 본페로니 검정만큼 많은 귀무가설을 기각시킨다. 왼쪽 그림에서, Tukey 검정은 본페로니보다 2개의 귀무가설을 더 잘 기각시켰다.
.....
=> Bonfferoni 검정, Holm 검정은 기각역이 작아 False positive(= Type I error)는 줄어들지만 False negative(= Type II error)를 유발하는 문제가 생긴다. 따라서 낮은 검정력으로 True positive를 놓치게 된다.
요약하면, 본페로니 검정과 holm 검정은 모든 다중 검정 상황에서 일반적으로 사용되는 방법이지만 특정 상황에서는 보다 더 높은 검정력을 가지면서 FWER을 통제하는 Tukey, Scheffe 검정이 이용될 수 있다는 것이다. 그리고 모든 개별 검정 유의수준을 동일하게 적용하는 것이 아닌 p-value의 크기 순서를 반영하여 개별 유의수준을 덜 보수적으로 작용하도록 하였다. 하지만, 이는 가설의 수(m)가 적은 상황에서는 합리적이지만, m=100 or m=1000 인 상황에서는 개별 유의 수준을 조정한다할지라도 매우 보수적일 수 밖에 없다. 즉, 귀무가설을 기각시키지 못하며, 이는 검정력이 낮다는 것과 일맥상통한다. 따라서, m이 클 때는 조금의 false positive를 감수하면서 true positive를 찾는 방법을 모색하게 되며, 이는 FDR의 모티베이션이 된다.
(2) FDR(False discovery rate)
FDR이란, FWER과는 다른 종류의 오류로 귀무가설을 기각시킨 결정 중 잘못 기각한 경우의 기대비율(= E(False positives/ Total positives))이며, 어느정도 false positive를 수용하면서 더 많은 true positive 을 찾는 것이 목적이다. 기대값을 씌우는 이유는 실제로 귀무가설이 참인지 거짓인지 V값을 알 수 없기 때문에 기댓값을 씌워 분석자가 수용할 수 있는 false positive의 수를 지정해주기 위함이다. 만약, FDR을 q = 20% 에서 통제한다는 의미는 평균적으로 기각된 귀무가설들 중 false positive(잘못된 판단)가 20% 이하가 되도록 보장하면서 가능한 많은 귀무가설을 기각한다는 것이다. 또 이는 기각된 귀무가설 중 20%가 false positive임을 의미한다. FDR을 통제하는 방법으로 Benjamini-Hochberg 검정을 제시한다.
- Benjamini-Hochberg 검정

개별 검정에 대한 p-값을 순차적으로 나열한 뒤 각각 다른 유의수준$\frac{i}{m}q$을 부여하는 방법이다. FWER에서 개별 검정의 adjusted p-value $\tilde{p}$를 제시해주듯이, FDR은 q-value 라는 측도를 제시해준다. q-value도 p-value에 기반한 값으로 FDR에서 제공하는 일종의 adjusted p-value라고 할 수 있다.
$\tilde{q_j} = ing \left \{q : H_0 \ regected \ at \ FDR \leq q \right \}$
inf는 infimum으로 하한을 말하며, $\tilde{q_j}$의 상한값은 항상 1이다. 위 수식의 해석은 "가설 j를 기각하는데에 필요한 FDR q수준의 하한이 q-value"이다. FWER처럼 $\alpha$를 조절하는 것이 아니므로 해석에는 주의가 필요하다. 예를 들어, q = 0.05는 귀무가설을 기각한 판단 중 잘못된 판단을 한 비율을 5% 이상으로 설정하면, 가설 j를 기각할 수 있다는 뜻이다. 즉, 해당 귀무가설보다 작은 p-값을 가지는 가설 중 false positive가 5% 정도가 있음을 감안하여 기각하는 것이다.

중간 그림은 FDR이 1%인 수준에서 검정을 수행할 때, 146개의 귀무가설이 기각되는 것을 보여주며, 오른쪽그림은 FDR이 3%인 수준에서 검정을 수행할 때, 279개의 귀무가설이 기각되는 것을 보여준다.
(참고)
* 유의수준과 FWER의 비교
alpha는 한 개의 가설에 대한 개념으로 가설검정 결과가 잘못된 판단일 최대 확률.
FWER은 여러 개의 가설에 대한 개념으로 가설검정 결과들 중 적어도 한 개의 가설이 잘못된 판단일 확률. 여기서 한 개의 가설마다 alpha의 개념은 똑같으며 FWER은 전체오류율로 생각하면됨.
참고문헌
https://be-favorite.tistory.com/20
#3 다중 검정
❗ Prerequisite 통계적 가설검정의 원리 다중 검정(multiple testing)은 여러 개의 검정을 동시에 수행하는 경우를 말한다. 이러한 경우에 단일 검정을 수행할 때와 똑같은 방식으로 검정을 진행하게
be-favorite.tistory.com
An Intriduction to Statistical Learning with Applications in R, Second Edition