재표본 방법에 기반한 검정(resampling, permutation)

 

확률변수 X는 처리군에 속한 쥐의 혈압 측정값을 의미하며, 확률변수 Y는 대조군에 속하는 귀의 혈압 측정값을 의미한다. 여기서 우리는 두 집단에 속한 쥐의 평균 혈압이 같은지 여부를 알고 싶고, two-sample t-test를 이용하여 검정을 수행한다. 가설은 다음과 같이 나타낼 수 있다. 

 

$H_0 : \mu_x = \mu_y$   vs    $H_1 : \mu_x \neq \mu_y$

$\mu_x = E(X) , \mu_y = E(Y)$

 

만약, $n_x$와 $n_y$가 크면, T통계량은 근사적으로 표준정규분포를 따른다. 하지만, 작은 경우 확률변수의 근사 분포 가정을 할 수 없기 때문에 T통계량의 귀무가설하에서의 분포를 알 수 없다. 이러한 경우, 우리는 재표본(re-sampling) 방법에 기반하여 T통계량의 근사적인 귀무가설 분포를 찾을 수 있다. 더 자세히 말하면, permutation 방법이라고 부른다. 

 

해당 방법은 귀무가설이 참인 경우를 생각하며 X와 Y의 분포가 같다는 가정을 하면, X와 Y가 섞인 데이터에 기반하여 구해진 T통계량의 분포와 원 데이터에 기반하여 구해진 T통계량과 같을 것이라는 아이디어에서 출발한다.

 

 

우선 랜덤하게 $n_x + n_y$개의 관측값들을 B번 재배치(permutation)한다. 여기서 B는 큰 값을 의미한다. 그리고 각 재배치를 수행할 때마다 T통계량($T^{*1}, \cdots, T^{*B}$)을 계산하며, 이들의 분포는 귀무가설하에서 T통계량의 근사 분포로 생각할 수 있다. 또한, 정의에 따라 p-값은 귀무가설하의 분포에서 검정 통계량보다 큰값을 관측할 확률을 의미한다. (또한, 귀무가설을 기각시켰을 때 그 판단이 잘못될 확률을 의미한다.)

 

예를 들어 설명해보자. 2종류의 혈액세포암을 가지는 환자($n_x = 29, n_y = 25$)를 대상으로 11번째 유전자의 평균 발현값이 같은지 T검정을 수행하려고 한다. 계산된 T 통계량은 -2.09 이며, 귀무가설하에서 자유도가 52인 t분포(이론적분포)를 사용했을 때 p-값은 0.041을 가진다. 만약, 재표본방법(B=10000)을 사용하여 귀무가설하의 근사분포를 이용했을 때 p-값은 = 0.047을 가진다. 즉, 11번째 유전자 평균 발현값은 두 환자 집단에서 같기 때문에 이론적분포를 사용했든 재표본방법을 사용하여 근사분포를 사용했든 차이가 없는 것을 알 수 있다. 

 

 

반대로, 유전자 평균 발현값이 두 환자 집단에서 다른 경우를 살펴보자. 877번째 평균 유전자 발현값이 두 환자 집단에서 다른지 T-검정을 수행한다. 이론적 분포하에서 계산된 p-값은 0.571, 재표본방법을 사용하여 귀무가설하의 근사분포를 이용했을 때 p-값은 0.673 으로 두 집단의 평균 유전자 발현값이 다르다고 할 수 있다. 또한, T-통계량의 근사분포와 이론적 분포를 나타내면 다음과 같으며, 877번째 유전자에 한해서 두 분포가 다른 것을 확인할 수 있다.

 

 

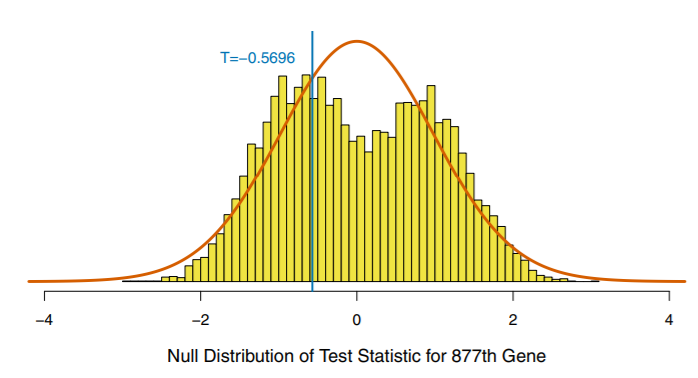
일반적으로 작은 샘플사이즈를 가지거나 치우쳐진 분포를 가지는 상황에서 재표본방법에 의한 근사분포의 p-값과 이론적분포의 p-값의 차이는 더 확실하게 나타날 것이다.