고윳값분해/스펙트럼분해/특잇값분해는 어떤 행렬을 고윳값과 고유벡터를 이용해 다른 형태로 표현하는 것이다. 이를 통해 행렬의 내부 구조를 살펴보거나 행렬을 이용한 연산을 더 효율적으로 할 때 유용하다.
(1) 고윳값(eigenvalue), 고유벡터(eigenvector)
p x p 정방행렬 A에 대해
$Av=\lambda v$
를 만족하는 0이 아닌 열벡터 $v$를 고유벡터, 상수 $\lambda$를 고윳값이라고 정의한다.


좀 더 정확한 용어로는 $\lambda$는 '행렬 A의 고윳값' , $v$는 '행렬 A의 $\lambda$에 대한 고유벡터' 이다.
고윳값과 고유벡터는 행렬에 따라 정의되는 값으로서 어떤 행렬은 이러한 고윳값-고유벡터가 존재하지 않을수도 있고 어떤 행렬은 하나만 존재하거나 또는 최대 p개까지 존재할 수 있다.
(2) 고유값, 고유벡터의 계산
다음의 관계
$Av=\lambda v $
$⇔ Av-\lambda v = 0 $ (0 : 영행렬)
$⇔ (A-\lambda E)v = 0$ (E : 단위행렬) ----- (1)
가 성립한다. 이를 만족하는 고유벡터 $v(\neq0)$가 존재하기 위해서는 다음을 만족해야 한다.
$det(A-\lambda E) = 0$ ----- (2)
(이 조건은 행렬 $A-\lambda E$가 역행렬이 존재하지 않는다는 뜻이다. 그 이유는 ($A-\lambda E$)의 역행렬이 존재한다면 $v$는 항상 $v=(A-\lambda E)^{-1} 0=0$ 만을 해로 가지므로.)
특성방정식이라 불리는 (2)를 $\lambda$에 대해 풀면 고윳값을 구할 수 있으며, 고유벡터는 구해진 고윳값을 식(1)에 대입하여 구하게 된다. 특정 고윳값에 대응하는 고유벡터는 유일하지 않다. 왜냐하면, 어떤 $v$가 고유벡터라 하면 이 벡터에 실수를 곱한 벡터 $cv$, 즉 $v$와 방향이 같은 벡터는 모두 고유벡터가 된다.
$Acv=\lambda cv $ ----- (3)
따라서 고유벡터는 식(3)과 같이 조건을 만족하는 벡터들 중에서 어느 벡터를 사용해도 무방하나 보통 크기를 1로 정규화한 단위벡터를 고유벡터로 사용하는 것이 일반적이다.
$\frac{v}{\left \| v \right \|}$
(3) 고윳값 분해(eigen decomposition)
행렬 A의 고윳값, 고유벡터들을 $\lambda_i$와 $v_i$라고 할 때, $Av_i=\lambda_i v (i=1,2,\cdots,p)$ 가 성립한다.

행렬 A의 고유벡터를 열벡터로 하는 행렬을 S, 고윳값을 대각원소로 하는 대각행렬을 $\Lambda $라고 할 때, 위 식은 다음과 같이 표현된다.
$AS=S\Lambda $
즉, $A = S\Lambda S^{1}$
위 결과를 고윳값분해라고 한다. 위 결과는 다시 $S^{-1}AS=\Lambda$을 의미하므로, "S가 행렬 A를 대각화함"을 의미한다. 모든 정방행렬이 고윳값분해가 가능한 것은 아니다. p*p 정방행렬 A가 고윳값분해가 가능하려면 행렬 A가 p개의 일차독립인 고유벡터를 가져야 한다. 고윳값들이 0을 포함하지 않으면 무조건 고유벡터들은 일차독립이다. 하지만 고윳값에 0이 포함되면 고유벡터들은 일차독립이 아니다. 일차독립(linearly indepenent)이란, 어떤 벡터들의 집합{v1,v2,...vp}이 있을 때 이들 벡터들 중 어느 한 벡터도 다른 벡터들의 상수배 합으로 표현될 수 없으면 이 벡터들을 서로 일차독립이라고 정의한다. 즉, ,행렬 A가 서로 다른 고윳값을 가지면, 선형독립인 p개의 고유벡터를 갖게 되어 고윳값분해(대각화)가 가능하다.
(4) 스펙트럼 분해(spectrum decomposition)
[대칭행렬(symmetric matrix)의 고유벡터 직교성(orthogonal)]
정방행렬들 중에서 대각원소를 중심으로 원소값들이 대칭되는 행렬 즉, $A=A^T$인 행렬을 대칭행렬이라 부른다.
대칭행렬은 고윳값 분해와 관련하여 좋은 성질 3가지를 가지고 있다. 대칭행렬은 항상 고윳값 대각화가 가능하며 더구나 직교행렬 대각화가 가능하다. 대각화는 분해와 같은 말로 생각하면 된다.
$A=P\Lambda P^{-1}$
$=P\Lambda P^T$
이 성질을 이용하면, 직교행렬 $P(PP^T=E)$ 와 대각행렬 $\Lambda$를 다음과 같이 $P=(e_1,e_2,\cdots,e_p), \Lambda=diag(\lambda_1,\lambda_2,\cdots,\lambda_p)$ 로 정의할 때, 다음의 스펙트럼 분해가 성립한다.
$A=P\Lambda P^T$
$A=\sum_{i=1}^{p} \lambda_i e_i e_i^T$
행렬 A의 고윳값들의 집합을 스펙트럼이라고 한다. $\lambda_i$는 A의 고윳값이고, $e_i$는 고윳값에 대응하는 단위 고유벡터이다.
즉, 모든 대칭행렬은 '직교행렬을 통한' 고윳값 대각화가 가능하다. 이 성질은 주성분분석(PCA), 특잇값분해(SVD) 등에서 가장 기본이 되는 성질로 활용된다.
모든 정방행렬이 고윳값 분해가 가능한 것은 아니지만 대칭행렬은 항상 고윳값 분해가 가능하며 더구나 직교행렬로 대각화가 가능함을 기억하자.
* 직교(orthogonal)와 정규직교(orthonormal), 그리고 직교행렬(orthogonal matrix)
두 벡터 v1,v2 가 서로 수직이면(즉, v1*v2=0) 두 벡터 v1,v2는 서로 직교하다고 한다. 그리고 v'=v/||v||와 같이 어떤 벡터를 크기가 1인 단위벡터로 만드는 것을 정규화(nomalization)라고 한다. 정규직교라는 말은 orthogonal 과 normal이 합쳐진 말로서 두 벡터 v1,v2가 모두 단위벡터(unit vector)이면서 서로 수직이면 두 벡터는 v1,v2는 정규직교 하다고 한다.
orthogonal, orthonormal은 벡터들 사이의 관계를 나타내는 말인데, 이게 행렬로 넘어가면 조금 의미가 달라진다.
먼저, 행렬에서는 직교행렬(orthogonal matrix)이라는 말은 있어도 정규직교(orthonormal matrix)이라는 말은 없다. 흔히 orthonormal matrix 라는 표현을 쓰는 이는 잘못된 것이며 orthogonal matrix(직교행렬)가 올바른 용어이다.
직교행렬의 수학적 정의는 자신의 전치행렬(transpose)를 역행렬로 갖는 정방행렬이다.
$A^{-1}=A^T$
$AA^T=E$
직교행렬의 열벡터들은 서로 정규직교한 성질을 가지고 있다. 즉, 직교행렬은 구성하는 열벡터를 v1,v2,...vn 라고 했을 때, 이들은 모두 단위벡터(unit vector)이면서 또한 서로 수직인 성질을 갖는다.
$||v_i||=1, i=1,2,...n$
$v_i*v_j=0, i \neq j$
이러한 성질은 열벡터가 아닌 행벡터들에 대해서도 동일하게 성립한다. (즉, 행벡터들도 서로 정규직교하다)
즉, 직교행렬(orthogonal matrix)은 그 행렬을 구성하는 열벡터(행벡터)들이 서로 수직(orthogonal)이면서 크기가 1인(normal) 행렬로도 정의될 수 있다.
(5) 특잇값분해(singular value decomposition, SVD)
특잇값분해는 고윳값분해와 마찬가지로 행렬을 대각화하는 방법이다. 고윳값분해는 정방행렬(m*m) 중에서도 일부 행렬, 스펙트럼분해는 대칭행렬($A^{-1}=A^T$)에 적용되는 반면, 특잇값분해는 직사각(m*n)행렬에 대해서도 적용되므로 활용도가 높다. 다변량 분석(PCA,다차원척도법 등), 데이터마이닝과 기계학습 드의 주요 알고리즘에 특잇값분해가 사용된다.
$A=U\Sigma V^T$
$U : m*m 직교행렬
$V : n*n 직교행렬
$\Sigma : m*n 직사각 대각행렬
(ⅰ) $AA^T = U(\Sigma\Sigma^T)U^T$
(ⅱ) $A^TA = V(\Sigma\Sigma^T)V^T$
U는 $AA^T$를 고윳값분해해서 얻어진 직교행렬로 T의 열벡터들을 A의 left singular vector라 부른다. 또한 V는 $AA^T$를 고윳값분해에서 얻어진 직교행렬로서 V의 열벡터들을 A의 right singular vector라 부른다. 행렬 $\Sigma$의 대각원소($\sigma$)는 $AA^T, A^T A$의 고윳값들의 제곱근으로 A의 특잇값이라고 한다. ($\sigma_1 \geq \sigma_2 \geq \sigma_3 \cdots \sigma_s \geq 0$)
행렬 A의 특잇값(singular value)을 $\sigma_i$, 좌특이벡터(left singular vector)을 $u_i$, 우특이벡터(right sigular vector)을 $v_i$라 했을 때 다음 식이 성립한다.
$Av_i=\sigma_i u_i$ , $1\leq i \leq s$
이 사실로부터 SVD는 다음과 같이 표현될 수 있다
$A=\sum_{i=1}^{s} \sigma_i u_i v_i^T$
(6) 특잇값분해의 기하학적 의미
행렬A를 통한 선형변환(Ax)는 벡터(x)에 대해 회전(rotation), 반사(reflection)의 작용을 한다. 이 과정은 직교행렬($V^T$)에 의해 회전되고, 대각행렬($\Sigma$)에 의해 스케일 변환된 후, 다시 직교행렬($U$)에 의해 회전되는 과정이 결과와 동일하다.

(7) Reduced SVD , 행렬근사, 데이터압축
아래와 같이 m*n 행렬 A를 SVD로 분해하는 것을 full SVD라 부른다. (단, m>n)
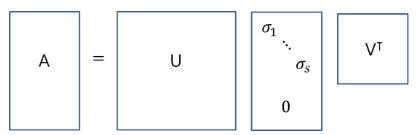
full SVD보다 다음과 같이 축소된 형태를 사용하는 것이 일반적이다. thin SVD는 $\Sigma$에서 비대각행렬이 0인 부분을 없애고 U에서는 이에 대응되는 열벡터들을 제거한 형태이고, compact SVD는 비대각,대각행렬이 0인 부분은 없앤 형태이다. truncated SVD는 특잇값이 큰 상위 t(<s)개만을 이용하는 분해로, 원 행렬 A를 A'로 근사하는 방법이다.



truncated SVD로 근사한 행렬 A'는 행렬노름(matrix norm) ||A-A'||을 최소화시키는 계수 t인 행렬로 데이터 압축, 노이즈 제거 등에 활용된다.
SVD가 활용되는 예로는 데이터 축소, 선형 최소제곱해 문제, 영상처리 및 압축, 잡음제거, 데이터 군집화에서 군집개수 결정, 다변량 이상치 참지, 관측값과 변수의 추세 참지, 행렬의 계수 결정 등이 있다.
출처 : https://darkpgmr.tistory.com/105
R 응용 다변량 분석 - 저자 : 나종화
'Multivariate analysis > 다변량분석' 카테고리의 다른 글
| Hotelling's T-Squared (0) | 2020.05.27 |
|---|---|
| ANOVA(분산분석), MANOVA(다변량분산분석) (0) | 2020.05.08 |
| 마할라노비스 제곱거리와 카이제곱분포을 통한 다변량 이상치 탐색 (0) | 2020.04.16 |
| 다변량 자료의 분산(일반화분산,총분산) / 선형관계(공분산,상관계수) (0) | 2020.04.01 |
| 거리 측도(유클리드, 맨하탄, 표준화, 마할노비스) (0) | 2020.04.01 |



댓글