1. Bias vs Variance
error = bias + variance =$Error(x) = (E[\hat{f}(x)]-f(x))^2+E[\hat{f}(x)-E[\hat{f}(x)]]^2+\sigma_e^2$
bias는 예측 평균값과 실제값의 차이를 제곱한 것으로 예측값이 실제값에서 떨어진 정도를 알 수 있다.
variance는 [예측값과 예측 평균값의 차이]의 제곱 평균으로 예측값들의 흩어진 정도를 나타낸다.
$\sigma_e^2$은 무슨 짓을 해도 줄일 수 없는 근본적이 오차를 의미한다. ( irreducible error )
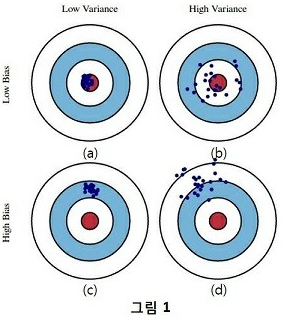
bias와 variance가 loss이므로, 직관적으로 둘 다 작은 (a)모델이 가장 좋은 모델이다. (b)모델은 예측값들의 평균값은 실제값과 비슷한데(bias 작음) 예측값의 variance는 커서 loss가 큰 모델이다. (c)모델은 bias가 크고 variance가 작다. (d)모델은 둘 다 크다.
2. Bias-Variance Trade-Off
bias가 커지면 variance가 작아지고 반대로 bias가 작아지면 variance가 커지는 Trade-off관계를 갖고 있다.
regression을 예로 들어보자. train data의 모든 점을 연결하게 위해 모델을 복잡(train data 내에 있는 에러나 노이즈까지 학습)하게 학습시켰다면 train error는 0이 될 것이다. 그러나, 이 모델에 test data를 fitting시키면 bias는 낮지만 variance는 커져 total error는 오히려 증가할 수 있습니다. 반대로, 모델 복잡도를 단순하게 가져가면 학습이 덜 되서 variance는 작은데 bias는 커져 total error가 증가할 수 있다. bias와 variance가 서로 상반되어 이를 bias-variance trade off라고 부른다.
3. Over-fitting , Under-fitting
train data로 모델을 학습시킨 후 test data로 fitting 했을 때, 위 그림(b),(c),(d)의 결과가 나올 수 있다. 왜 그럴까 ?
(1) 모델 복잡도가 높아지면(= training set을 매우 잘 학습) training set에 대해서는 매우 높은 성능을 보이지만, test set에 대해서는 정확도가 떨어지는 over-fitting(과대적합)이 발생한다.
- bias는 작으나 variance가 커진다.
(2) 모델이 단순해지면(= training set 충분히 학습 못함) test set 뿐만 아니라, training set에서 조차도 성능이 낮은 under-fitting(과소적합)이 발생한다.
- variance는 작으나 bias가 커진다.

'Statistics > ISLR' 카테고리의 다른 글
| Ridge / Lasso regression (0) | 2021.05.21 |
|---|---|
| 6. Linear Model Selection and Regularization (0) | 2020.10.25 |
| 3. Linear regression(선형 회귀) (0) | 2020.10.08 |
| Resampling Method(Hold-out, Cross-Validation, Bootstrap) (0) | 2020.10.05 |
| Introduction to Statistical Learning with R (0) | 2020.08.31 |




댓글