데이터가 정상성을 가지지 않으면 분석이 어렵기 때문에 정상성을 갖도록 만드는 전처리를 하게 된다. 보통 평균이 일정하지 않으면 차분을 취하고, 분산이 일정하지 않으면 변환을 취한다.
1. 정상성 데이터, 비정상성 데이터
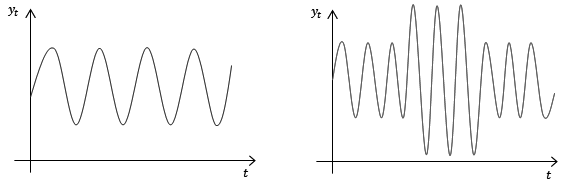
시계열 자료($y_t$)의 평균과 분산이 t시점에 상관없이 동일할 때와 $y_t와 y_{t-h}$시점의 자기 상관(시점간의 상관관계)은 시차(h)에만 의존하며 시점(t/t-h)에는 의존하지 않을 때 정상성(Stationarity)를 갖는다고 한다. 따라서, 추세나 계절성이 있는 시계열은 정상시계열이 아니다. (서로 다른 시점의 값에 영향을 줌).
* 정상성 가정에는 독립성 가정이 포함되어 있지 않음에 유의 !!
정상시계열 비정상시계열


2. 백색잡음(White Noise)
정상시계열의 대표적인 예로 백색잡음(white noise)가 있다. 백색잡음은 시점에 상관없이 평균이 0이고 분산이$\sigma^2$인 시계열자료를 일컷는다. 이를 확률변수 관점으로 표현하면, $\epsilon$(백색잡음)는 평균이 일정(보통 0으로 가정)하고 분산$\sigma^2$을 가지는 무상관인 확률변수로 정의된다.
$y_t=\epsilon_t ~ WN(0,\sigma^2)$
백색잡음의 평균과 분산은 각각 0, $\sigma^2$이므로 시점t에 영향을 받지 않음을 알 수 있다. 자기 공분산은 다음과 같으며 시점 t와 무관하므로 정상성을 만족하는 정상(stationary) 시계열이다.
$Cov(\epsilon_t, \epsilon_{t-h}) = \left\{\begin{matrix}
\sigma^2 ,h=0
\\0 , h\neq0
\end{matrix}\right. $
3. 확률보행(Random Walk)
비정상시계열의 대표적인 예로 확률보행(random walk)가 있다. 확률보행은 임의의 방향으로 향하는 연속적인 걸음을 나타낸다는 의미로 예측 불가능한 변동이 발생하는 것을 뜻한다. 위로갈 확률이나 아래로갈 확률이 같기 때문에 미래 이동을 예측할 수 없기 때문에 확률보행 모델에서 예측값은 마지막 예측값과 같다고 가정한다.
$y_t = y_{t-1} +\epsilon_t, \epsilon_t ~ iid(0,\sigma^2)$
* 확률보행모델의 오차항은 백색잡음이 아니다. 오차항의 분포에 대한 가정이다. but, 백색잡음이라고 가정할 경우, $y_t-y_{t-1}$ : 1차 차분 시계열은 백색잡음이다.
확률보행의 평균과 분산을 구해보면, 편의상 $y_0$=0이라고 할 때,
$E(y_t)=E(\epsilon_1+\epsilon_2+\dots + \epsilon_t)=0$
$Var(y_t)=Var(\epsilon_1)+Var(\epsilon_2)+\dots + Var(\epsilon_t) = t\sigma^2$
$Cov(y_t,y_s)=\min(t,s)\sigma^2$
확률보행과정은 분산이 시점 t에 의존하므로 비정상(non-stationary) 시계열임을 알 수 있다.
출처 : R 응용 시계열분석 (저자:나종화)
'Time Series analysis' 카테고리의 다른 글
| 개입분석(intervention analysis) (0) | 2020.12.11 |
|---|---|
| 전이함수모형(transfer function) (0) | 2020.11.24 |
| ARIMA 오차 회귀 모형 (0) | 2020.11.23 |
| 시계열 검정 (자기상관 검정, 단위근 검정, 정상성 검정) (0) | 2020.10.25 |
| 시계열(time series) (0) | 2020.09.14 |

댓글