DTW(Dynamic Time Warping)

Dynamic Time Warping에서 와핑(warping)의 사전적의미는 뒤틀림, 휨 이라는 뜻을 가지고 있으며, 동적 시간 와핑은 이름과 같이 '속도 또는 길이에 따라 움직임이 다른 두 시계열간의 유사성(거리)을 측정'하는 알고리즘으로, 그 거리가 최소화되는 방향으로 매칭시켜 누적 거리가 최소가 되는 warping(뒤틀림) 경로를 찾는다. DTW는 주로 그래픽, 비디오, 오디오와 같은 분야에서 사용되며, 의료분야에서 보행 유사성, 생체신호 분석에 사용되기도 한다. 특히, 자동음성 인식 분야에서 두각을 보이며 다른 속도를 가지는 음성을 인식하도록 해준다. 예를 들어, 두 사람의 걸음에 대한 유사성을 계산해보자. 두 사람의 걸음 패턴은 속도, 폭 등의 이유로 다르게 나타날 것이다.

https://en.wikipedia.org/wiki/Dynamic_time_warping

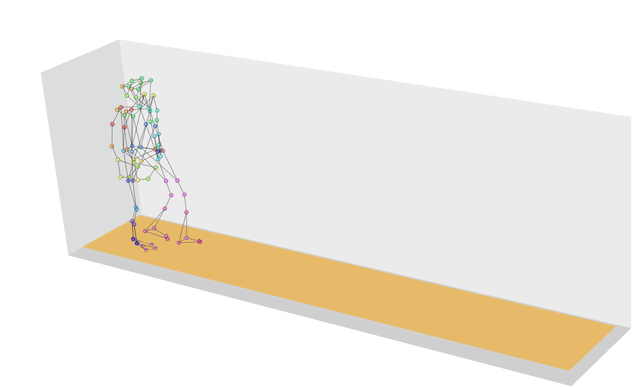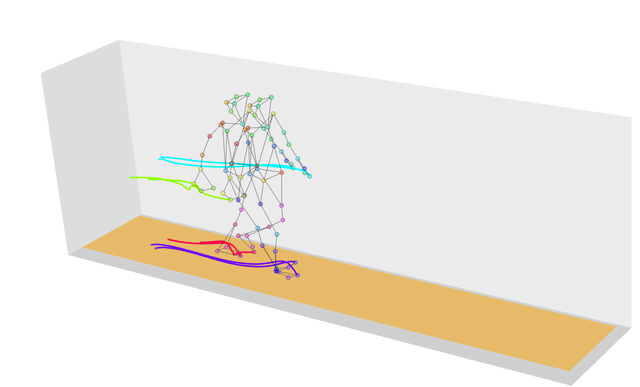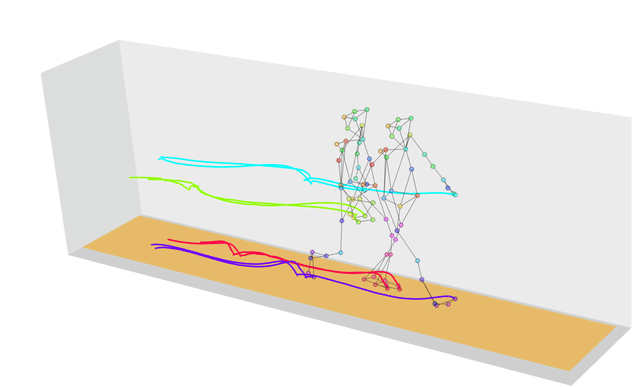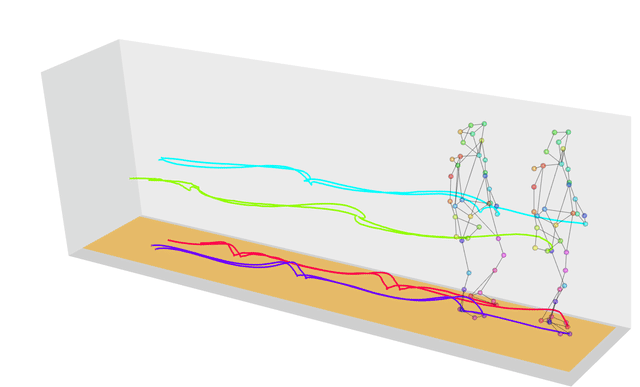
이러한 경우, 우리가 일반적으로 두 시계열 신호간 유사성을 따질 때 사용하는 측도인 유클리드 거리를 사용하게 되면, 같은 시간선상에 대해 거리를 계산하게 된다. 즉, 0초-0초, 1초-1초. 하지만, 그렇게 되면 아래의 왼쪽 그림과 같이 전반적으로 패턴이 비슷해 보이는 데이터에서 신호의 떨림과 움직임이 심해질수록 유사성을 찾을 수 없게 된다. 또한, 길이가 다른 시계열은 측정할 수 없다는 단점이 있다.

 

https://www.cs.ucr.edu/~eamonn/KAIS_2004_warping.pdf

 

이러한 문제는 DTW를 이용하여 해결할 수 있다. DTW의 아이디어는 동일한 시간선상의 데이터 뿐 아니라 주변 시점까지 비교 대상으로 사용하여 더 비슷한 요소와 매칭하는 것이다. 이제부터 DTW 알고리즘이 작동하는 원리에 대해 알아보자.

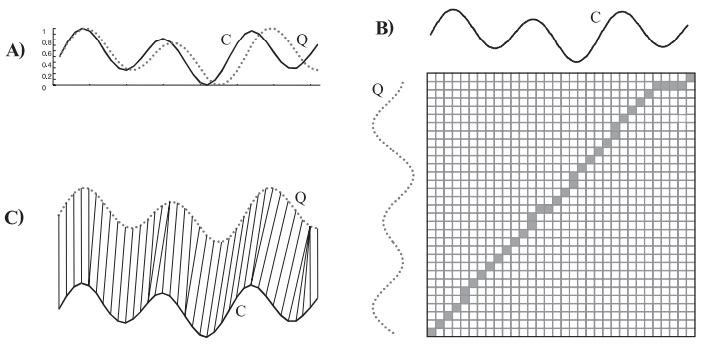
A) 길이가 각각 m, n인 두 개의 시계열 $Q = (q_1, q_2, \cdots, q_m)$, $C = (c_1, c_2, \cdots, c_n)$ 이 있다고 해보자. B) 먼저, 두 시계열을 나열하여 $m \times n$ 행렬을 만든다. 이 행렬의 (i, j)번째 요소는 두 점 $q_i$와 $c_j$ 간의 유클리드 거리 $d(q_i, c_j) = (q_i-c_j)^2$를 의미하며, 이를 이용하여 최적의 와핑 경로를 탐색한다. C) 와핑 경로(warping path) W는 Q와 C사이의 맵핑을 나타내는 와핑 거리의 집합이며, 연속적이여야 한다.

$W = w_1, w_2, \cdots, w_K$, $max(m,n) \leq K < m+n-1$

 

W에서 k번째 요소는 $w_k=(i, j)_k$로 정의되며, 이를 와핑 거리라고 한다. 이 때 W는 다음의 3가지 조건을 만족해야한다.

 

• Boundary conditions : $w_1 = (1,1)$와 $w_K = (m,n)$는 이어져야한다. 즉, 시작점과 끝점은 $w_1 = (1,1)$와 $w_K = (m,n)$이어야한다.
• Continuity : $w_k = (a,b)$와 $w_k = (a', b')$에서 $a-a' \leq 1, b-b' \leq 1$이어야 한다. 즉, 와핑 경로는 대각 요소를 포함한 인접한 셀로 제한된다.
• monotonicity : $w_k = (a,b)$와 $w_{k-1} = (a',b')$에서 $a-a' \geq 0, b-b' \geq 0$이어야 한다. 즉, 와핑 경로는 음의 방향으로 이동하지 않는다.

 

 

https://www.cs.ucr.edu/~eamonn/KAIS_2004_warping.pdf

위의 3가지 조건을 만족하는 와핑 경로들 중에서 와핑 거리$w_k$들의 총합이 최소가 되는 경로를 찾는 것이 목적이다. 우리는 이를 와핑 경로 비용(warping path cost)이라고 부르기도 하며, 와핑 경로 비용이 최소가 되는 경로를 찾는 것과 같다.

$DTW(Q, C) = min \left \{\frac{1}{K}\sqrt{\sum_{k=1}^K w_k} \right.$

 

여기서, K는 서로 다른 길이를 가지고 있는 와핑 경로들에 대한 보상을 위해 사용된다. i=j=0에서부터 시작하여 k번째 와핑 거리$w_k$의 누적 와핑 거리 $D(i,j)$는 아래 식으로 정의할 수 있다. 식의 의미는 [i 번째 요소와 j 번째 요소의 거리] + [(i,j)번째 요소의 거리에 인접한 셀까지의 누적거리 중 최솟값] 으로 결국 최단거리방향으로 진행하는 것을 의미한다.

누적 와핑 거리 $D(i,j)$는 $i=j=0$에서부터 시작하며, 최종적인 유사도를 나타내는 값은 위의 DTW(Q, C)의 값과 같게 된다.

 

$D(i,j) = d(q_i, c_j) + min \begin{pmatrix}
D(i-1, j-1)\\
D(i-1, j)\\
D(i, j-1)
\end{pmatrix}$

 

 

지금까지 DTW에 대하여 공부했으니 실제 데이터를 이용하여 직접 계산해보자. 이후 글을 천천히 다시 읽어보면 이해가 될 것이다.

 

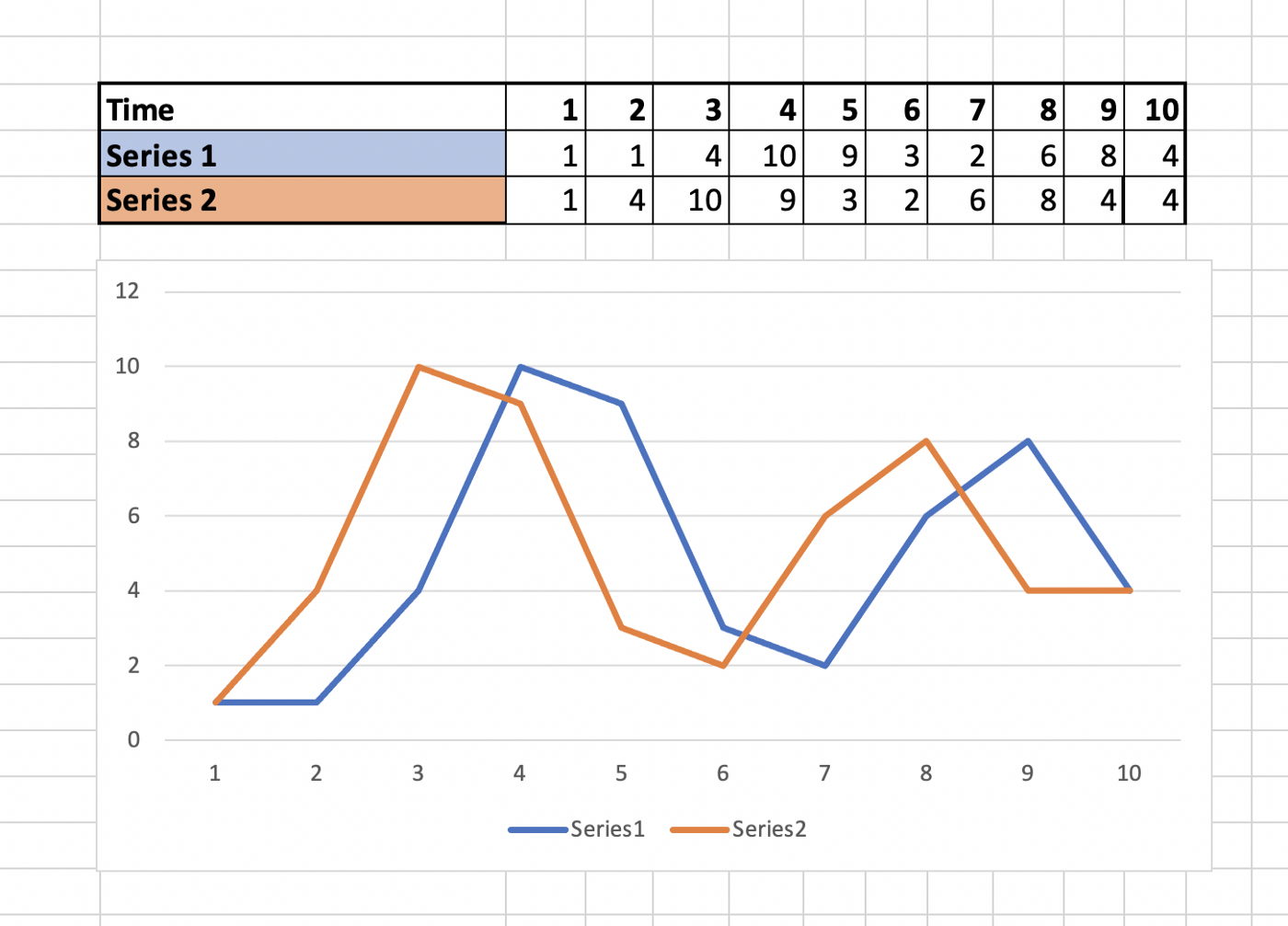
1.  길이가 같은 두 개의 시계열 자료 P, Q 가 있다고 하자.

2. 두 시계열을 나열하여 10 $times$ 10 행렬을 생성한다. 우리는 이를 Cost Matrix 라고 한다.

3. Cost Matrix 의 각 셀은 누적 와핑 거리를 의미하며 다음의 식을 통해 계산된다.

$D(i,j) = d(p_i, q_j) + min \begin{pmatrix}
D(i-1, j-1)\\
D(i-1, j)\\
D(i, j-1)
\end{pmatrix}$

계산 과정을 보기 위해 계산된 몇 개의 요소(11, 3, 8)를 살펴보자.

• (4, 4) 번째 요소인 11

      =  |10 - 4| + min(5, 12, 5) = 6 + 5

• (2, 1) 번째 요소인 3

      =  |4 - 1| + min(0) = 3

• (1, 3) 번째 요소인 8

      = |1 - 3| + min(6) = 8


4. 모두 계산된 Cost Matrix 는 다음과 같다.

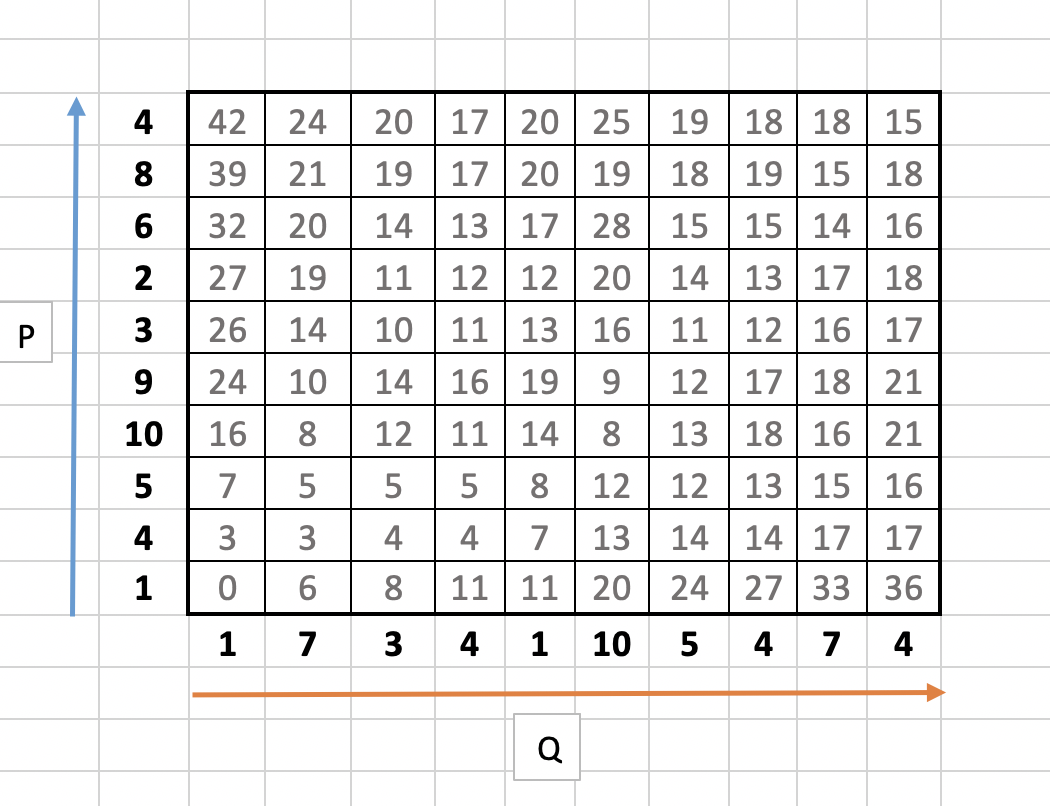
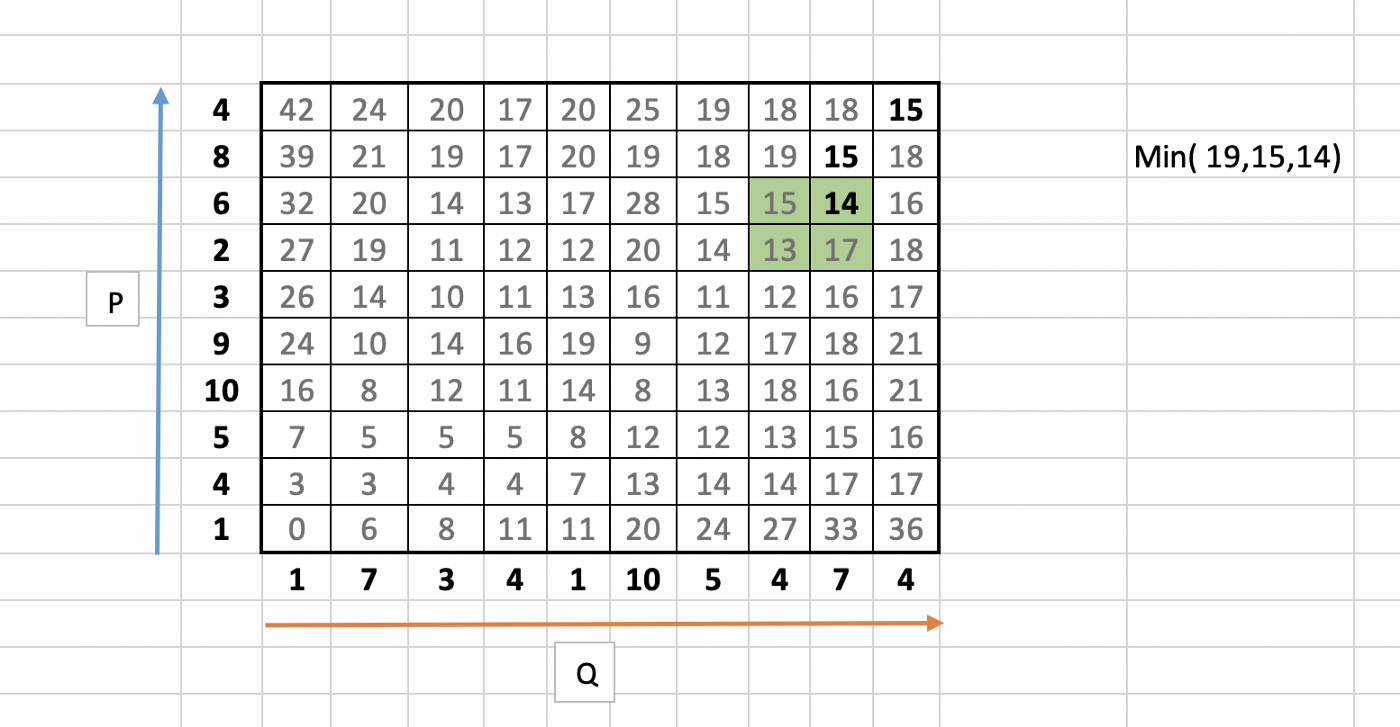
5. 최적의 와핑 경로는 누적 와핑 거리가 최소가 되는 경로이며, 맨 오른쪽 상단의 지점부터 맨 왼쪽 하단의 거리까지 탐색을 시작한다. 탐색 대상은 시작 지점의 주변이며, 15의 주변인 (15, 18, 18) 가 된다.

 

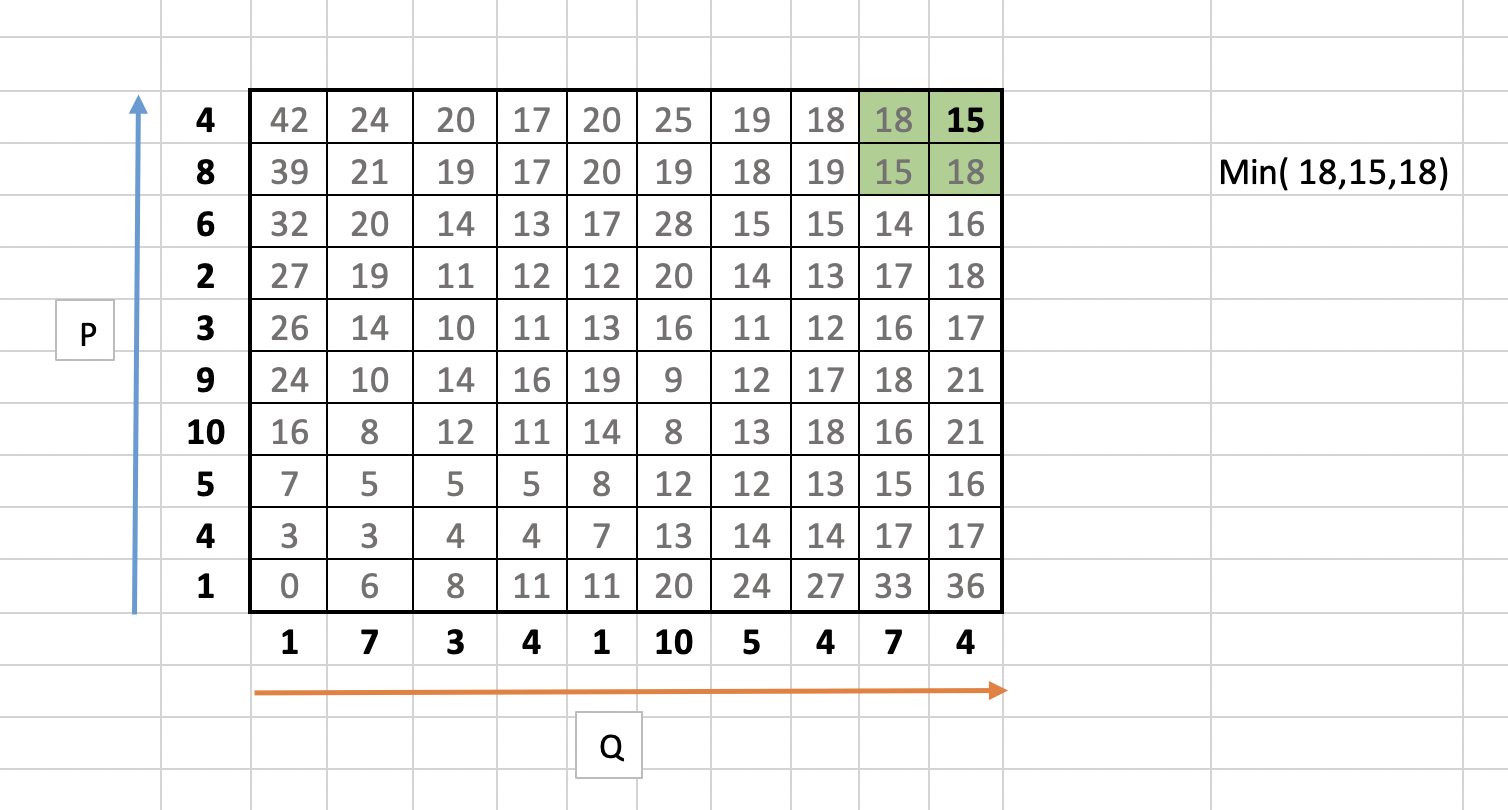
6. 그 중 최소값인 15을 선택하며, 선택된 15의 주변을 탐색한다.

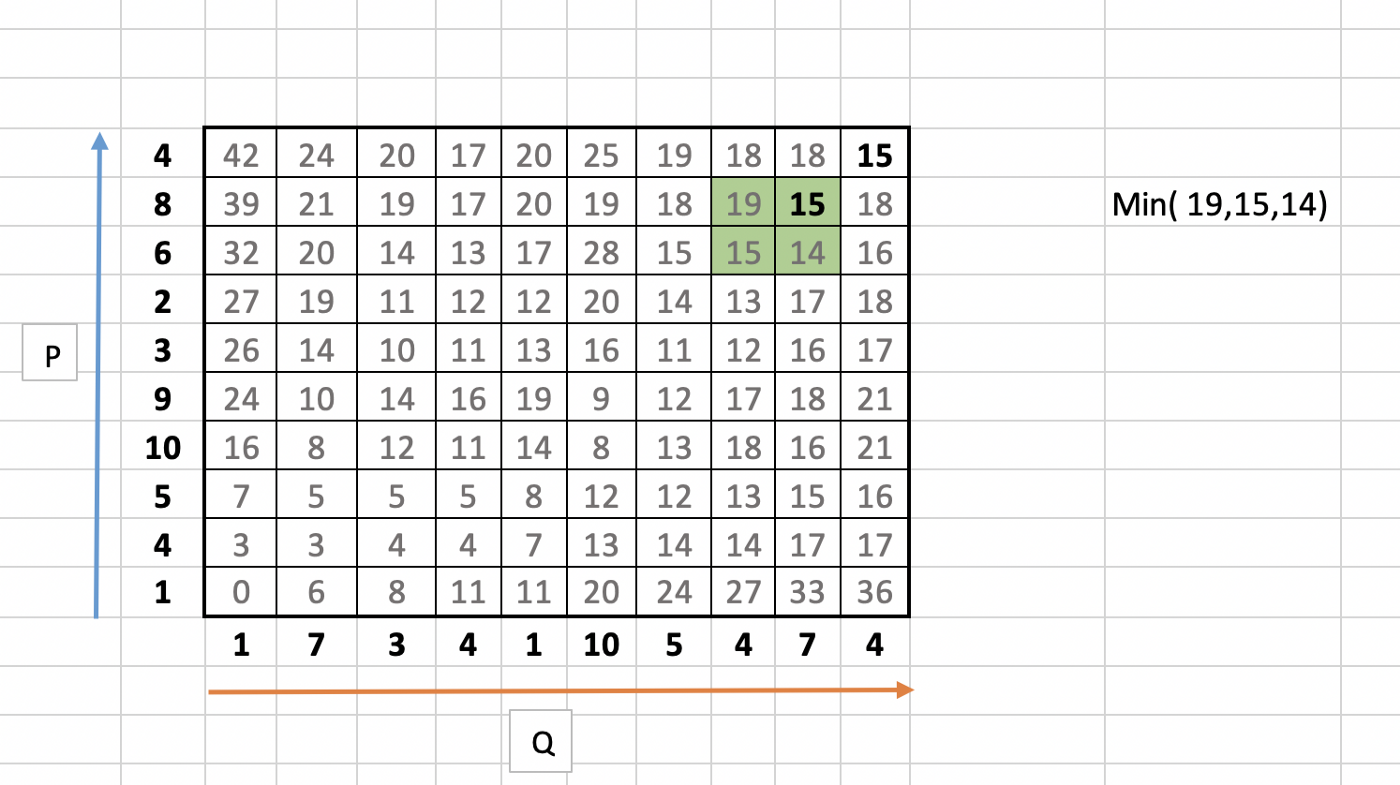
7. 15의 주변은 (15, 19, 14) 이며 그 중 최솟값인 14 를 선택한다. 이러한 과정을 거쳐 맨 왼쪽 하단까지 진행을 한다.

최종 경로는 다음과 같다.

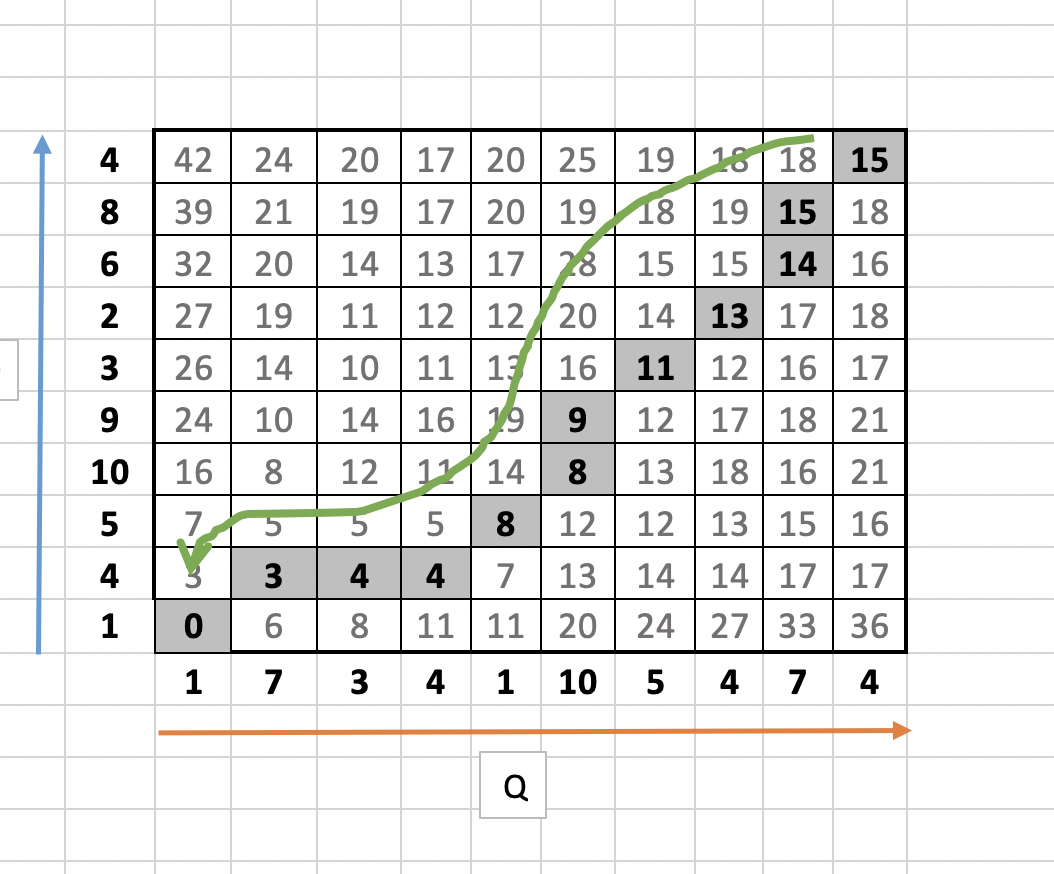
W = [15, 15, 14, 13, 11, 9, 8, 8, 4, 4, 3, 0]


8. 최종 선택된 와핑 경로 비용(= 와핑 거리의 총합)은 다음과 같다.

DTW(Q, C) = [15 + 15 + 14 + 13 + 11 + 9 + 8 + 8 + 4 + 4 + 3 + 0] / 12

 

이번에는 패턴이 같은 두 시계열 자료에 대해 시간 차이만 두는 예제를 생각해보자. Cost Matrix 와 와핑 경로는 다음과 같다.

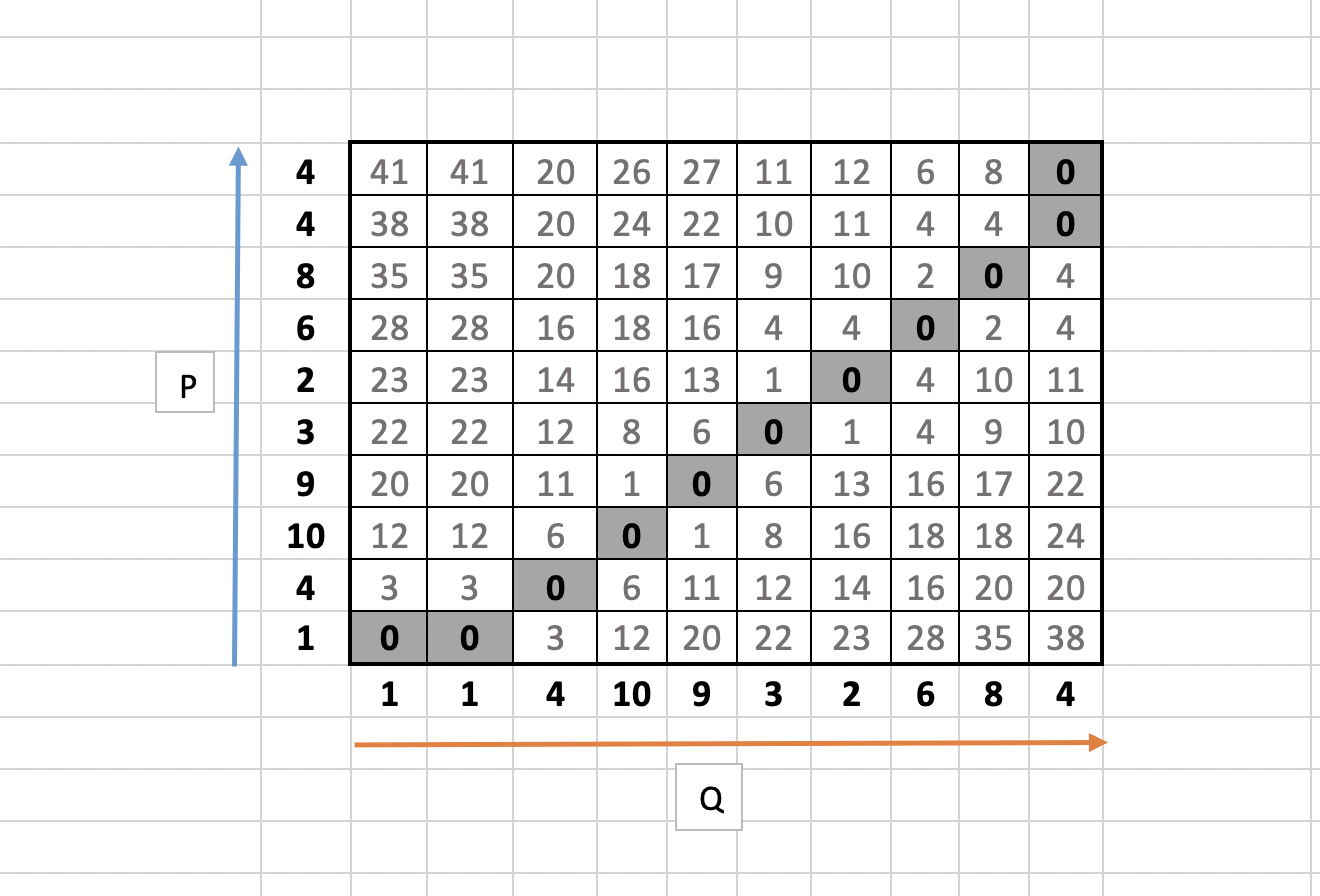
DTW(P, Q) = [0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0] / 11 = 0 이며, 이는 두 시계열이 같은 패턴을 가지고 있음을 의미한다.

 

 

 

 

 

 

 

 

참고문헌 

 

https://medium.com/walmartglobaltech/time-series-similarity-using-dynamic-time-warping-explained-9d09119e48ec

Time Series Similarity Using Dynamic Time Warping -Explained

https://leo-bb.tistory.com/58

[시계열/python]Python을 이용한 Dynamic Time Wraping(DTW)