이전 포스팅에서 다루었던 DTW는 '속도 또는 길이에 따라 움직임이 다른 두 시계열간의 유사성(거리)을 측정'하는 알고리즘이라고 소개하였다. 많은 분야에서 DTW가 사용되고 있지만, DTW 알고리즘에는 다음의 2가지 알려진 문제점이 있다.
- 와핑경로(Warping path) 계산 시에 특이점(Singularities)이 발생한다.
- DTW 알고리즘을 통해 계산된 와핑경로가 올바른지 알 수 없다.
1. 특이점(Singularities)
첫번째 문제로 언급한 특이점은 다음의 상황을 일컫는다.

특이점이란, 위의 그림에서 박스친 부분과 같이 한 패턴(시계열자료)에서 여러 개의 점이 다른 패턴의 한 점에 집중되는 현상을 말한다. 이 특이점은 한 시계열 패턴이 굴곡을 가지는 경우 즉, X(시점) 값에 대한 Y(시계열 자료) 값이 다른 경우에 나타나게 된다. 즉, DTW는 time delay 된 자료에 대해 잘 적합하기 때문에 만약 다른 한 패턴이 독자적으로 감소하거나 증가하는 패턴(local feature)을 가진다면, 이를 잘 매칭하기 위해 특이점이 발생하게 된다. 일반적으로 거리가 잘 매칭되는 이상적인 그림은 한 점에 다수의 점이 매칭이 되는 것이 아닌 여러 점이 각자 잘 매칭이 되는 것이다.

위의 그림 중 b, d 는 a 와 c 자료에 대해 각각 DTW를 적용한 것이며, 두 시계열의 패턴이 같은 경우, b 와 같은 경로가 나타나게 된다. 반면, c 처럼 한 시계열 패턴에서 약간의 굴곡이 존재하면, d 와 같은 특이점이 발생한다.
2. 특이점 문제를 완화
DTW는 두 점의 Y값만 고려하여 최소가 되는 거리를 매칭하기 때문에 추세를 고려하지 않아 이와같은 특이점이 발생하게 된다. 이러한 특이점 문제는 1978년도에 Sakoe, & Chiba에 의해 발표되었으며, 특이점을 완화시키는 몇몇 방법들이 제안되었다. 이에 대해서 간단히 다뤄보자.
1) Windowing : 와핑 경로가 갈 수 있는 공간을 제한하는 방법으로 특이점의 최대 갯수를 제한 할 수 있으나, 특이점 자체가 발생하는 문제를 막을 순 없다. 아래의 그림에서 2개의 점선이 와핑 경로가 나아가는 방향을 제한하는 역할을 수행하며, 다음의 식으로 제한된 구역을 나타낼 수 있다.
|i-(n/(m/j))| < R, where R is a positive integer window width.

2) Slope Weighting : DTW의 누적 거리 D(i,j) 방정식을 다음의 식으로 대체하는 방법이다. X축의 값을 반영함으로써 뒤틀린 정도를 억제할 수 있다. X가 커질수록 경로는 대각선 방향을 띠게 된다.
$D(i,j) = d(q_i, c_j) + min \begin{pmatrix}
D(i-1, j-1)\\
X D(i-1, j)\\
X D(i, j-1)
\end{pmatrix}$
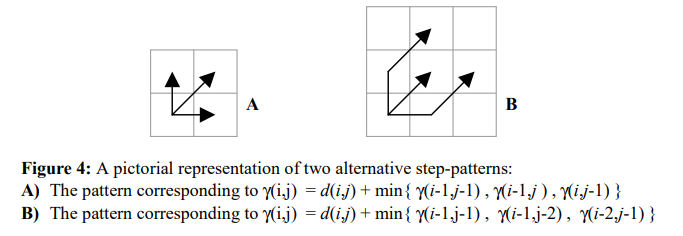
3) Step Patterns (Slope constraints) : DTW의 와핑경로가 나아가는 단계-페턴은 그림 A와 같이 나타낼 수 있었다. 제안된 방법은 다음의 방정식을 사용하며,
$D(i,j) = d(q_i, c_j) + min \begin{pmatrix}
D(i-1, j-1)\\
X D(i-1, j-2)\\
X D(i-2, j-1)
\end{pmatrix}$
와핑 경로가 나아갈 수 있는 단계-패턴은 그림 B와 같이 나타낼 수 있다. 이런 단계-패턴은 와핑 경로가 각 단계에서 대각선 방향으로 무조건 한단계씩 이동하도록 한다.
위의 방법들은 특이점 문제를 완화시켜주지만, 올바른 와핑 경로를 놓칠 위험이 있다. 또한, 1,2번 방법에서 매개변수(R, X)와 step-pattern을 선택하는 방법은 명확하게 제시되어 있지 않다.
3. Derivate DTW
특이점 문제를 해결하기 위한 다른 방안으로 DDTW가 있다. DTW는 Y값만을 고려하여 문제가 발생한다고 하였다. 따라서, 제안된 DDTW는 두 점의 Y 값을 고려하지 않는 방식으로 DTW를 개선시킨 방법이며, shape을 고려한다. shape을 고려한다는 말은 즉 추세를 고려한다는 의미를 가진다. 1차 미분을 통해 자료의 shape에 대한 정보를 얻을 수 있다. 따라서, 우리는 제안된 방법을 Derivative Dynamic Time Warping (DDTW)라고 부른다.
DTW에서 우리는 두 점 Q, C 사이의 유클리드 거리 $d(q_i, c_i)$를 계산한 $n \times m$ 행렬을 구성하였다. 이에 DDTW는 $d(q_i, c_i)$를 유클리드 거리 행렬 대신 $q_i$와 $c_i$의 추정된 1차 미분값 차이의 제곱 값을 사용한다. 미분값을 추정하는 방법이 존재하지만, 단순화와 일반화를 위해 다음의 식을 사용한다.
$D_x(q) = \frac{(q_i - q_{i-1}) + ((q_{i+1} - q_{i-1})/2)}{2}$ , $1<i<m$
위의 추정치에 대해 설명하면, [(i-1)번째 값과 i 번째 값의 기울기 + (i+1)번째 값과 (i-1)번째 값의 기울기] 의 평균을 의미한다. (This estimate is simply the average of the slope of the line through the point in question and its left neighbor, and the slope of the line through the left neighbor and the right neighbor.)
경험적으로 위의 추정치는 두 점의 Y값만을 고려하는 거리 측도보다 이상치(outlier)에 더 유연(robust)하다. 위의 추정치는 첫번째 점과 마지막 점을 고려하지 않는 점에 유의하자. 또한, 잡음이 존재하는 데이터에 대해서는 미분값을 추정하기 전에 지수평활(exponential smoothing)을 먼저 수행한 후 진행한다. DDTW의 계산량은 DTW와 동일하게 mn이며, 단순히 미분값을 계산하는 과정만 추가된 것이다.
DTW를 최적화시킨 많은 방법들이 제안되어 왔으며, 이는 DDTW에도 동일하게 잘 적용된다.

결측된 구간의 이전 t-T , t-1 시점을 Q로 두고 Q와 가장 패턴이 비슷한 구간을 전체 구간에서 탐색하여 선택된 구간 이후의 패턴을 복사함.
DTWBI는 이전 포스팅에서 다루었던 DTW을 이용하여 단일 시계열에서 발생한 결측값을 대치하는 방법이다. 다음의 시계열 자료가 존재하며, [t, t+T-1] 시점에서 크기가 T 인 결측이 발생한 것을 볼 수 있다. 결측이 발생한 시점 t 에서 T시점 이전부터 t-1 시점까지의 구간을 Q라고 하고 전제 구간에서 Q와 유사한 구간을 찾아 그 구간 이후의 자료를 결측값으로 대치한다. 즉, 결측이 발생한 구간의 이전 패턴과 비슷한 패턴이 시계열 자료에 있을 것이라고 가정하고 비슷한 패턴을 찾아 이후의 데이터를 복사하는 것이다. 이 때 비슷한 패턴을 가지는 구간은 DTW 원리를 이용한다.
'Time Series analysis' 카테고리의 다른 글
| 개입분석(intervention analysis) (0) | 2020.12.11 |
|---|---|
| 전이함수모형(transfer function) (0) | 2020.11.24 |
| ARIMA 오차 회귀 모형 (0) | 2020.11.23 |
| 시계열 검정 (자기상관 검정, 단위근 검정, 정상성 검정) (0) | 2020.10.25 |
| 정상시계열과 비정상시계열 (0) | 2020.10.07 |

댓글